Comparative study of unsupervised dimension reduction techniques for the visualization of microarray gene expression data

Abstract

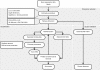
Background: Visualization of DNA microarray data in two or three dimensional spaces is an important exploratory analysis step in order to detect quality issues or to generate new hypotheses. Principal Component Analysis (PCA) is a widely used linear method to define the mapping between the high-dimensional data and its low-dimensional representation. During the last decade, many new nonlinear methods for dimension reduction have been proposed, but it is still unclear how well these methods capture the underlying structure of microarray gene expression data. In this study, we assessed the performance of the PCA approach and of six nonlinear dimension reduction methods, namely Kernel PCA, Locally Linear Embedding, Isomap, Diffusion Maps, Laplacian Eigenmaps and Maximum Variance Unfolding, in terms of visualization of microarray data.

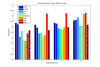
Results: A systematic benchmark, consisting of Support Vector Machine classification, cluster validation and noise evaluations was applied to ten microarray and several simulated datasets. Significant differences between PCA and most of the nonlinear methods were observed in two and three dimensional target spaces. With an increasing number of dimensions and an increasing number of differentially expressed genes, all methods showed similar performance. PCA and Diffusion Maps responded less sensitive to noise than the other nonlinear methods.

Conclusions: Locally Linear Embedding and Isomap showed a superior performance on all datasets. In very low-dimensional representations and with few differentially expressed genes, these two methods preserve more of the underlying structure of the data than PCA, and thus are favorable alternatives for the visualization of microarray data.

Figure 1

Benchmark. Our benchmark, consisting of three independent procedures. (1) Dimension reduction: Every dataset is mapped into a low-dimensional target space. All necessary parameters are determined by a loo-cv with a SVM. (2) Classification: Every dataset is classified by a SVM with Gaussian kernel during 100 randomization steps. A gradient descend procedure estimates all SVM parameters. (3) Cluster validation: The Davis-Bouldin-Index measures the distance between labeled clusters within the low-dimensional data.

Figure 2

Visualization. Two dimensional visualization example of the Haferlach et al. Leukemia dataset. The LLE and Isomap embedding show more distinct clusters than the first two principal components of a PCA.

Figure 3

Randomization accuracies. Support Vector Machine classification accuracies of the Wang et al. breast cancer dataset. The data was randomized a hundred times for fixed target space dimensions two (left) and three (center) and for dimensions estimated by loo-cv (right). In the last case, the plot also shows the results for the original high-dimensional data without reduction. Especially in two and three dimensions, all nonlinear methods are superior to PCA.

Figure 4

Cluster validation. Davis-Bouldin-Indices of the reduced Wang et al. breast cancer dataset for fixed target space dimensions 2,3,5 and 10. In most cases, the nonlinear methods produce more distinct clusters than PCA.

Figure 5

Noise evaluation. Randomization accuracies (left) and cluster-indices (right) for the Wang et al. breast cancer dataset combined with normally distributed noise with zero mean and different variances. PCA and DM react most stable on noise. All other methods lead to varying accuracies and cluster scores.

Figure 6

Simulated data. Leave-one-out cross-validation accuracies of the simulated datasets with increasing differential features. The red line marks the average accuracy of all 100 generated datasets within the 95% quantile. In two dimensional target spaces, LLE an IM capture more of the underlying structure of the data with much fewer significant features than PCA.