Parallel MR image reconstruction using augmented Lagrangian methods
- PMID: 21095861
- PMCID: PMC3081617
- DOI: 10.1109/TMI.2010.2093536
Parallel MR image reconstruction using augmented Lagrangian methods
Abstract
Magnetic resonance image (MRI) reconstruction using SENSitivity Encoding (SENSE) requires regularization to suppress noise and aliasing effects. Edge-preserving and sparsity-based regularization criteria can improve image quality, but they demand computation-intensive nonlinear optimization. In this paper, we present novel methods for regularized MRI reconstruction from undersampled sensitivity encoded data--SENSE-reconstruction--using the augmented Lagrangian (AL) framework for solving large-scale constrained optimization problems. We first formulate regularized SENSE-reconstruction as an unconstrained optimization task and then convert it to a set of (equivalent) constrained problems using variable splitting. We then attack these constrained versions in an AL framework using an alternating minimization method, leading to algorithms that can be implemented easily. The proposed methods are applicable to a general class of regularizers that includes popular edge-preserving (e.g., total-variation) and sparsity-promoting (e.g., l(1)-norm of wavelet coefficients) criteria and combinations thereof. Numerical experiments with synthetic and in vivo human data illustrate that the proposed AL algorithms converge faster than both general-purpose optimization algorithms such as nonlinear conjugate gradient (NCG) and state-of-the-art MFISTA.
Figures
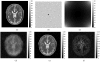

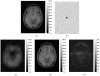


References
-
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity Encoding for Fast MRI. Magnetic Resonance in Medicine. 1999;42:952–962. - PubMed
-
- Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in Sensitivity Encoding with Arbitrary k-Space Trajectories. Magnetic Resonance in Medicine. 2001;46:638–651. - PubMed
-
- Lin FH, Kwong KK, Belliveau JW, Wald LL. Parallel Imaging Reconstruction Using Automatic Regularization. Magnetic Resonance in Medicine. 2004;51:559–567. - PubMed
-
- Qu P, Luo J, Zhang B, Wang J, Shen GX. An Improved Iterative SENSE Reconstruction Method. Magnetic Resonance Engineering. 2007;31:44–50.
-
- Lin FH, Wang FN, Ahlfors SP, Hamalainen MS, Belliveau JW. Parallel MRI Reconstruction Using Variance Partitioning Regularization. Magnetic Resonance in Medicine. 2007;58:735–744. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

