Modeling the spread of vector-borne diseases on bipartite networks

Abstract

Background: Vector-borne diseases for which transmission occurs exclusively between vectors and hosts can be modeled as spreading on a bipartite network.

Methodology/principal findings: In such models the spreading of the disease strongly depends on the degree distribution of the two classes of nodes. It is sufficient for one of the classes to have a scale-free degree distribution with a slow enough decay for the network to have asymptotically vanishing epidemic threshold. Data on the distribution of Ixodes ricinus ticks on mice and lizards from two independent studies are well described by a scale-free distribution compatible with an asymptotically vanishing epidemic threshold. The commonly used negative binomial, instead, cannot describe the right tail of the empirical distribution.

Conclusions/significance: The extreme aggregation of vectors on hosts, described by the power-law decay of the degree distribution, makes the epidemic threshold decrease with the size of the network and vanish asymptotically.

Figure 1. Dependence of the epidemic threshold on the network size for various degree distributions (logarithmic scale on both axes).

The circles represent the epidemic threshold from our simulation, and the lines the predictions obtained with Eq.1. Colors refer to combinations of degree distributions. Blue: Poisson distribution for both hosts and vectors; red: Poisson distribution for vectors, scale-free () for hosts.

Figure 2. Distribution of the number of ticks on hosts for the Slovakia and Tuscany datasets.

The line represents the power-law distribution with parameters and determined by Maximum Likelihood Estimation.

Figure 3. The dependence of the Vuong -statistic on the degree threshold for the Slovakia and Tuscany datasets.

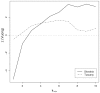
Positive (negative) values of imply that the data are better described by the power law (negative binomial) distribution. While the whole distribution is better described by the negative binomial, the power law is a better fit to the large- behavior, which governs the asymptotic behavior of the epidemic threshold.

Figure 4. Dynamics of the fraction of infected nodes at constant transmission probability.

The networks follow a scale-free degree distribution with for the hosts and a Poisson degree distribution for the vectors. As the number of hosts is increased, the epidemic is sustained for longer times.