Confidence from uncertainty--a multi-target drug screening method from robust control theory

Abstract

Background: Robustness is a recognized feature of biological systems that evolved as a defence to environmental variability. Complex diseases such as diabetes, cancer, bacterial and viral infections, exploit the same mechanisms that allow for robust behaviour in healthy conditions to ensure their own continuance. Single drug therapies, while generally potent regulators of their specific protein/gene targets, often fail to counter the robustness of the disease in question. Multi-drug therapies offer a powerful means to restore disrupted biological networks, by targeting the subsystem of interest while preventing the diseased network from reconciling through available, redundant mechanisms. Modelling techniques are needed to manage the high number of combinatorial possibilities arising in multi-drug therapeutic design, and identify synergistic targets that are robust to system uncertainty.

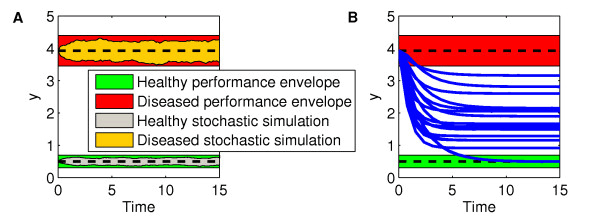
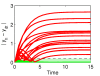
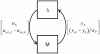
Results: We present the application of a method from robust control theory, Structured Singular Value or μ- analysis, to identify highly effective multi-drug therapies by using robustness in the face of uncertainty as a new means of target discrimination. We illustrate the method by means of a case study of a negative feedback network motif subject to parametric uncertainty.

Conclusions: The paper contributes to the development of effective methods for drug screening in the context of network modelling affected by parametric uncertainty. The results have wide applicability for the analysis of different sources of uncertainty like noise experienced in the data, neglected dynamics, or intrinsic biological variability.

Figure 1

Range of applicability of SSV analysis for robust therapy design. Once a model has been established that satisfactorily explains the dynamics of the diseased state, SSV analysis can be used to identify potent and robust multi-drug therapy candidates. SSV analysis first identifies which therapies can best manipulate the protein(s) of interest. Then, the candidate list is further filtered to therapies which are robust to known or perceived uncertainty affecting the treatment. The uncertainty may include parameter uncertainty and uncertainty generated during model development, but also disturbances occurring during the actual treatment, such as failure to properly adhere to a drug regimen schedule.

Figure 2

Case study model. (A) Topology of the network. U is the enzyme catalyzing the conversion of X to product Y, through the intermediate UX. The open arrows indicate the chemical reactions, and the oval arrow a negative regulation. k's represent the parameters involved in each step. Ø is the null component to indicate production and degradation. Input to the system is given by the total enzyme, U_tot, concentration, constant over time and given by u_tot = u+ux (lower-case component names indicate the corresponding concentrations). Output of the system is y. Inputs and outputs are highlighted in red. (B) Nonlinear model equations. The reaction rates are given by mass-action, negative feedback is described by the multiplicative term containing k₅. The nominal values of the parameters are: k₁ = 1, k₂ = 2, k₃ = 10, k₄ = 0.5, k₅ = 0.5, k_-1 = 3, k_-3 = 1.

Figure 3

Performance envelopes and therapeutic fitting. (A) Temporal simulation of the nonlinear model in Figure 2B with nominal parameters, under healthy conditions (u_tot,h = 0.2, and initial conditions given by the healthy steady-state), and diseased conditions (u_tot,d = 2, and initial conditions given by the diseased steady-state). Performance envelopes are generated to contain the stochastic envelopes, resulted by the Stochastic Simulation Algorithm (mean ± standard deviation). Nominal results are also shown in dashed lines. (B) Comparison between the performance envelopes and the results obtained from the nonlinear model, starting from the diseased steady-state, with parameter values modified according to the 56 therapies (blue curves).

Figure 4

Nominal performance analysis results. Trajectories obtained with the nonlinear deviation model for each of the 56 therapies without parametric uncertainty. Green and red lines denote therapies that pass and do not pass the nominal performance selection criterion, respectively. The performance envelope is shaded in light green.

Figure 5

Block diagram representation of the deviation models. The deviation model is shown in M-Δ form. The vector of input and output between the two blocks are also indicated. u_Δ and y_Δ represent the uncertain components of the input and output, respectively, for the system M.

Figure 6

Robust performance analysis and results of one robust therapy in presence of parametric uncertainty. (A) Results of the SSV analysis applied for robust performance, in presence of parametric uncertainty. Green and red dots illustrate therapies that pass and do not pass the robust performance selection criterion, respectively. (B) Comparison between the performance envelopes described in Figure 3A and the results obtained from therapy no. 30. Blue curves are the simulation results by therapy 30 linearized model with 100 different parameter sets, sampled within ± 45% of the nominal values. Gray curves are the upper and lower bounds of the stochastic envelope generated by the Stochastic Simulation Algorithm of therapy 30 nonlinear model (mean ± standard deviation of 100 trajectories).

Figure 7

Local sensitivity analysis results. Sensitivity coefficients, S_i, of the diseased output at steady-state, y_ss,d, respect to the parameter indicated on the x-axis. The coefficients are normalized with the nominal value of each parameter and with the steady-state output concentration y_ss,d.