Sensitivity analysis of dynamic biological systems with time-delays

Abstract

Background: Mathematical modeling has been applied to the study and analysis of complex biological systems for a long time. Some processes in biological systems, such as the gene expression and feedback control in signal transduction networks, involve a time delay. These systems are represented as delay differential equation (DDE) models. Numerical sensitivity analysis of a DDE model by the direct method requires the solutions of model and sensitivity equations with time-delays. The major effort is the computation of Jacobian matrix when computing the solution of sensitivity equations. The computation of partial derivatives of complex equations either by the analytic method or by symbolic manipulation is time consuming, inconvenient, and prone to introduce human errors. To address this problem, an automatic approach to obtain the derivatives of complex functions efficiently and accurately is necessary.

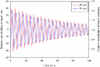
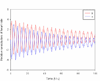
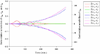
Results: We have proposed an efficient algorithm with an adaptive step size control to compute the solution and dynamic sensitivities of biological systems described by ordinal differential equations (ODEs). The adaptive direct-decoupled algorithm is extended to solve the solution and dynamic sensitivities of time-delay systems describing by DDEs. To save the human effort and avoid the human errors in the computation of partial derivatives, an automatic differentiation technique is embedded in the extended algorithm to evaluate the Jacobian matrix. The extended algorithm is implemented and applied to two realistic models with time-delays: the cardiovascular control system and the TNF-α signal transduction network. The results show that the extended algorithm is a good tool for dynamic sensitivity analysis on DDE models with less user intervention.

Conclusions: By comparing with direct-coupled methods in theory, the extended algorithm is efficient, accurate, and easy to use for end users without programming background to do dynamic sensitivity analysis on complex biological systems with time-delays.

Figure 1

Stacked 100% column chart for individual state variables. Each column in the stack column chart shows all relative parameter sensitivities for a state variable. The proportion of a parameter sensitivity to the total sensitivity for a state variable is displayed as a color area in each column. The values of time-averaged relative parameter sensitivities are used as the data.

Figure 2

The relative sensitivities of heart rate and blood pressure with respect to p₀. The relative sensitivities of heart rate and blood pressure with respect to the uncontrolled average arterial blood pressure. The time is in dimensionless scale.

Figure 3

The relative sensitivities of heart rate with respect to β and ν. The relative sensitivities of heart rate with respect to parameters for slow sympathetic control and fast vagal control. The time is in dimensionless scale.

Figure 4

The relative sensitivities of blood pressure with respect to β and ν. The relative sensitivities of blood pressure with respect to parameters for slow sympathetic control and fast vagal control. The time is in dimensionless scale.

Figure 5

Schematic diagram of TNF-α signal transduction network. The solid lines indicate reversible reactions and the dash-dot lines denote irreversible reactions. The dash lines indicate the delayed transcription processes. The reactions and components of the survival pathway are shown in green. The reactions and components of the apoptotic pathway are shown in blue. The boxes with red border denote the components with nonzero initial value in the network.

Figure 6

Stacked 100% column chart for individual state variables. Each column in the stack column chart shows all semi-relative parameter sensitivities for a state variable. The proportion of a parameter sensitivity to the total sensitivity for a state variable is displayed as a color area in each column. The values of time-averaged semi-relative parameter sensitivities are used as the data.

Figure 7

The symmetry of semi-relative sensitivities with respect to k₉ and k₁₅. The solid lines are the semi-relative sensitivities with respect to the rate constant k₉ of the formation of survival complex and the short dash lines are the semi-relative sensitivities with respect to the rate constant k₁₅ of the formation of death complex. The semi-relative sensitivities of NF-κB (x₁₆) are shown in red, IκB (x₃₁) in green, activated caspase-3 (x₂₅) in blue, and fragmented DNA (x₂₆) in pink.

Figure 8

The semi-relative sensitivities of fragmented DNA. The semi-relative sensitivities of fragmented DNA (x₂₆) with respect to the rate constants of the formation of survival complex (k₉), the formation of death complex (k₁₅), the formation of DISC without TNFR1 (k₁₇), the caspase-8 activation (k₂₀), the cleavage of procaspase-3 (k₂₁), the caspase-3 activation (k₂₃), and the fragmentation of DNA (k₂₆).

Figure 9

The semi-relative sensitivities of NF-κB. The semi-relative sensitivities of NF-κB (x₁₆) with respect to the rate constants of the formation of survival complex (k₉), the IKK activation (k₁₁), the formation of NF-κB/IκB/IKK* (k₁₂), the NF-κB activation (k₁₄), the formation of death complex (k₁₅), the deactivation of NF-κB (k₂₈), and the transcription of cIAP and IκB (k₂₉).

Figure 10

The semi-relative sensitivities of DISC. The semi-relative sensitivities of DISC (x₂₁) with respect to the rate constants of the formation of survival complex (k₉), the formation of death complex (k₁₅), the formation of DISC without TNFR1 (k₁₇ ), the caspase-8 activation (k₂₀).

Figure 11

The relative sensitivities obtained by the finite difference method and the EAMCM method. a) The relative sensitivities of heart rate with respect to the uncontrolled average arterial blood pressure (β); b) The relative sensitivities of blood pressure with respect to β. The green and red lines are obtained by the finite difference method with spacing ratio 0.1 and 0.01, respectively. The blue line is obtained by the EAMCM method. The time is in dimensionless scale.