The Binding Energy Distribution Analysis Method (BEDAM) for the Estimation of Protein-Ligand Binding Affinities
- PMID: 21116484
- PMCID: PMC2992355
- DOI: 10.1021/ct1002913
The Binding Energy Distribution Analysis Method (BEDAM) for the Estimation of Protein-Ligand Binding Affinities
Abstract
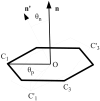
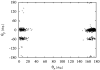
The Binding Energy Distribution Analysis Method (BEDAM) for the computation of receptor-ligand standard binding free energies with implicit solvation is presented. The method is based on a well established statistical mechanics theory of molecular association. It is shown that, in the context of implicit solvation, the theory is homologous to the test particle method of solvation thermodynamics with the solute-solvent potential represented by the effective binding energy of the protein-ligand complex. Accordingly, in BEDAM the binding constant is computed by means of a weighted integral of the probability distribution of the binding energy obtained in the canonical ensemble in which the ligand is positioned in the binding site but the receptor and the ligand interact only with the solvent continuum. It is shown that the binding energy distribution encodes all of the physical effects of binding. The balance between binding enthalpy and entropy is seen in our formalism as a balance between favorable and unfavorable binding modes which are coupled through the normalization of the binding energy distribution function. An efficient computational protocol for the binding energy distribution based on the AGBNP2 implicit solvent model, parallel Hamiltonian replica exchange sampling and histogram reweighting is developed. Applications of the method to a set of known binders and non-binders of the L99A and L99A/M102Q mutants of T4 lysozyme receptor are illustrated. The method is able to discriminate without error binders from non-binders, and the computed standard binding free energies of the binders are found to be in good agreement with experimental measurements. Analysis of the results reveals that the binding affinities of these systems reflect the contributions from multiple conformations spanning a wide range of binding energies.
Figures



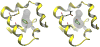





References
Grants and funding
LinkOut - more resources
Full Text Sources
