Semi-isometric registration of line features for flexible fitting of protein structures
- PMID: 21124809
- PMCID: PMC2993115
- DOI: 10.1111/j.1467-8659.2010.01813.x
Semi-isometric registration of line features for flexible fitting of protein structures
Abstract
In this paper, we study a registration problem that is motivated by a practical biology problem - fitting protein structures to low-resolution density maps. We consider registration between two sets of lines features (e.g., helices in the proteins) that have undergone not a single, but multiple isometric transformations (e.g., hinge-motions). The problem is further complicated by the presence of symmetry in each set. We formulate the problem as a clique-finding problem in a product graph, and propose a heuristic solution that includes a fast clique-finding algorithm unique to the structure of this graph. When tested on a suite of real protein structures, the algorithm achieved high accuracy even for very large inputs containing hundreds of helices.
Figures




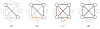


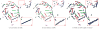

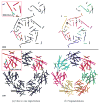
References
-
- Aiger D, Mitra NJ, Cohen-Or D. 4-points congruent sets for robust pairwise surface registration. ACM Transactions on Graphics (TOG) 2008 August;27(3):1–10.
-
- Au O K-C, Tai C-L, Cohen-Or D, Zheng Y, Fu H. Computer Graphics Forum (Proc of Eurographics 2010) IEEE; 2010. Electors voting for fast automatic shape correspondence.
-
- Berman H, Henrick K, Nakamura H. Announcing the worldwide protein data bank. Nature Structural Biology. 2003;10(12):980–980. - PubMed
-
- Besl PJ, McKay ND. A method for registration of 3-d shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992 February;14(2):239–256.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
