Zipf's law leads to Heaps' law: analyzing their relation in finite-size systems
- PMID: 21152034
- PMCID: PMC2996287
- DOI: 10.1371/journal.pone.0014139
Zipf's law leads to Heaps' law: analyzing their relation in finite-size systems
Abstract
Background: Zipf's law and Heaps' law are observed in disparate complex systems. Of particular interests, these two laws often appear together. Many theoretical models and analyses are performed to understand their co-occurrence in real systems, but it still lacks a clear picture about their relation.
Methodology/principal findings: We show that the Heaps' law can be considered as a derivative phenomenon if the system obeys the Zipf's law. Furthermore, we refine the known approximate solution of the Heaps' exponent provided the Zipf's exponent. We show that the approximate solution is indeed an asymptotic solution for infinite systems, while in the finite-size system the Heaps' exponent is sensitive to the system size. Extensive empirical analysis on tens of disparate systems demonstrates that our refined results can better capture the relation between the Zipf's and Heaps' exponents.
Conclusions/significance: The present analysis provides a clear picture about the relation between the Zipf's law and Heaps' law without the help of any specific stochastic model, namely the Heaps' law is indeed a derivative phenomenon from the Zipf's law. The presented numerical method gives considerably better estimation of the Heaps' exponent given the Zipf's exponent and the system size. Our analysis provides some insights and implications of real complex systems. For example, one can naturally obtained a better explanation of the accelerated growth of scale-free networks.
Conflict of interest statement
Figures

 . The Heaps' exponents
. The Heaps' exponents  for the numerical results of Eq. 6 and the simulation results of the stochastic model are obtained by using the least square method.
for the numerical results of Eq. 6 and the simulation results of the stochastic model are obtained by using the least square method.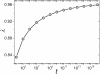
 .
.
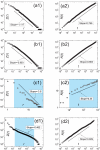
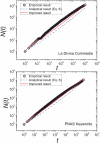
 is the frequency of the word ranked
is the frequency of the word ranked  and
and  is the number of distinct words. (b) Keywords of articles published in the Proceedings of the National Academy of Sciences of the United States of America (PNAS) where
is the number of distinct words. (b) Keywords of articles published in the Proceedings of the National Academy of Sciences of the United States of America (PNAS) where  is the frequency of the keyword ranked
is the frequency of the keyword ranked  and
and  is the number of distinct keywords; (c) Confirmed cases of the novel virus influenza A (H1N1) where
is the number of distinct keywords; (c) Confirmed cases of the novel virus influenza A (H1N1) where  is the number of confirmed cases of the country ranked
is the number of confirmed cases of the country ranked  and
and  is the number of infected country in the presence of
is the number of infected country in the presence of  confirmed cases over the world; (d) PNAS articles having been cited at least once from 1915 to 2009 where
confirmed cases over the world; (d) PNAS articles having been cited at least once from 1915 to 2009 where  is the number of citations of the article ranked
is the number of citations of the article ranked  and
and  is the number of distinct articles in the presence of
is the number of distinct articles in the presence of  citations to PNAS. In (c), the data set is small and thus the effective number is only two digits. The fittings in (c1) and (c2) only cover the area marked by blue. In (d1), the deviation from a power law is observed in the head and tail, and thus the fitting only covers the blue area. The Zipf's (power-law) exponents and Heaps' exponents are obtained by using the maximum likelihood estimation
, and least square method, respectively. Statistics of these data sets can be found in Table 1 (the data set numbers of (a), (b), (c) and (d) are 9, 10, 34 and 35 in Table 1) with detailed description in
Materials and Methods
.
citations to PNAS. In (c), the data set is small and thus the effective number is only two digits. The fittings in (c1) and (c2) only cover the area marked by blue. In (d1), the deviation from a power law is observed in the head and tail, and thus the fitting only covers the blue area. The Zipf's (power-law) exponents and Heaps' exponents are obtained by using the maximum likelihood estimation
, and least square method, respectively. Statistics of these data sets can be found in Table 1 (the data set numbers of (a), (b), (c) and (d) are 9, 10, 34 and 35 in Table 1) with detailed description in
Materials and Methods
.
 are given as 1.117 and 0.893, respectively.
are given as 1.117 and 0.893, respectively.
 ,
,  and
and  . The system sizes (i.e., the total number of word occurrences), from left to right, are
. The system sizes (i.e., the total number of word occurrences), from left to right, are  ,
,  and
and  . Fitting exponent
. Fitting exponent  is obtained by the least square method. The fitting lines and numerical results almost completely overlap.
is obtained by the least square method. The fitting lines and numerical results almost completely overlap.References
-
- Zipf GK. Human Behaviour and the Principle of Least Effort: An introduction to human ecology (Addison-Wesly, Cambridge) 1949.
-
- Heaps HS. Information Retrieval: Computational and Theoretical Aspects (Academic Press, Orlando) 1978.
-
- Clauset A, Shalizi CR, Newman MEJ. Power-law distributions in empirical data. SIAM Rev. 2009;51:661–703.
-
- Axtell RL. Zipf Distribution of U.S. Firm Sizes. Science. 2001;293:1818–1820. - PubMed
-
- Drăgulescu A, Yakovenko VM. Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Physica A. 2001;299:213–221.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

