Emergent properties of tumor microenvironment in a real-life model of multicell tumor spheroids
- PMID: 21152429
- PMCID: PMC2994713
- DOI: 10.1371/journal.pone.0013942
Emergent properties of tumor microenvironment in a real-life model of multicell tumor spheroids
Abstract
Multicellular tumor spheroids are an important in vitro model of the pre-vascular phase of solid tumors, for sizes well below the diagnostic limit: therefore a biophysical model of spheroids has the ability to shed light on the internal workings and organization of tumors at a critical phase of their development. To this end, we have developed a computer program that integrates the behavior of individual cells and their interactions with other cells and the surrounding environment. It is based on a quantitative description of metabolism, growth, proliferation and death of single tumor cells, and on equations that model biochemical and mechanical cell-cell and cell-environment interactions. The program reproduces existing experimental data on spheroids, and yields unique views of their microenvironment. Simulations show complex internal flows and motions of nutrients, metabolites and cells, that are otherwise unobservable with current experimental techniques, and give novel clues on tumor development and strong hints for future therapies.
Conflict of interest statement
Figures
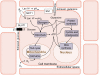

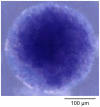
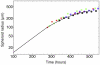
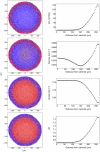
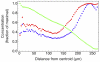
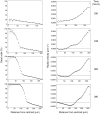
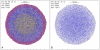
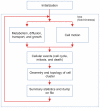

 variables), convergence is fast, because the initial concentration values are invariably very close to the final ones.
variables), convergence is fast, because the initial concentration values are invariably very close to the final ones.References
-
- Sutherland RM. Cell and environment interactions in tumor microregions: the multicell spheroid model. Science. 1988;240:177–84. - PubMed
-
- Bjerkvig R. Spheroid Culture in Cancer Research. Boca Raton, Fla.: CRC Press; 1992.
-
- Mueller-Klieser W. Three-dimensional cell cultures: from molecular mechanisms to clinical applications. Am J Physiol. 1997;273:C1109–23. - PubMed
-
- Mueller-Klieser W. Tumor biology and experimental therapeutics. Crit Rev Oncol Hematol. 2000;36:123–39. - PubMed
-
- Gottfried E, Kunz-Schughart LA, Andreesen R, Kreutz M. Brave little world: spheroids as an in vitro model to study tumor-immune-cell interactions. Cell Cycle. 2006;5:691–695. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

