Attention, uncertainty, and free-energy
- PMID: 21160551
- PMCID: PMC3001758
- DOI: 10.3389/fnhum.2010.00215
Attention, uncertainty, and free-energy
Abstract
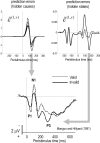
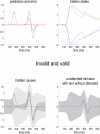
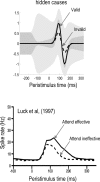
We suggested recently that attention can be understood as inferring the level of uncertainty or precision during hierarchical perception. In this paper, we try to substantiate this claim using neuronal simulations of directed spatial attention and biased competition. These simulations assume that neuronal activity encodes a probabilistic representation of the world that optimizes free-energy in a Bayesian fashion. Because free-energy bounds surprise or the (negative) log-evidence for internal models of the world, this optimization can be regarded as evidence accumulation or (generalized) predictive coding. Crucially, both predictions about the state of the world generating sensory data and the precision of those data have to be optimized. Here, we show that if the precision depends on the states, one can explain many aspects of attention. We illustrate this in the context of the Posner paradigm, using the simulations to generate both psychophysical and electrophysiological responses. These simulated responses are consistent with attentional bias or gating, competition for attentional resources, attentional capture and associated speed-accuracy trade-offs. Furthermore, if we present both attended and non-attended stimuli simultaneously, biased competition for neuronal representation emerges as a principled and straightforward property of Bayes-optimal perception.
Keywords: attention; biased competition; free-energy; generative models; perception; precision; predictive coding.
Figures

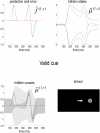
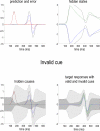
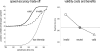
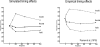
References
-
- Adams W. J., Graf E. W., Ernst M. O. (2004). Experience can change the ‘light-from-above’ prior. Nat. Neurosci. 7, 1057–1058 - PubMed
-
- Alais D., Burr D. (2004). The ventriloquist effect results from near-optimal bimodal integration. Curr. Biol. 14, 257–262 - PubMed
-
- Anderson A. J., Carpenter R. H. S. (2006). Changes in expectation consequent on experience, modeled by a simple, forgetful neural circuit. J. Vis. 6, 822–835 - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources

