Comparison of multi-subject ICA methods for analysis of fMRI data
- PMID: 21162045
- PMCID: PMC3117074
- DOI: 10.1002/hbm.21170
Comparison of multi-subject ICA methods for analysis of fMRI data
Erratum in
-
Correction to "Comparison of multi-subject ICA methods for analysis of fMRI data".Hum Brain Mapp. 2024 Aug 15;45(12):e70006. doi: 10.1002/hbm.70006. Hum Brain Mapp. 2024. PMID: 39183477 Free PMC article. No abstract available.
Abstract
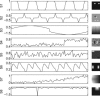
Spatial independent component analysis (ICA) applied to functional magnetic resonance imaging (fMRI) data identifies functionally connected networks by estimating spatially independent patterns from their linearly mixed fMRI signals. Several multi-subject ICA approaches estimating subject-specific time courses (TCs) and spatial maps (SMs) have been developed, however, there has not yet been a full comparison of the implications of their use. Here, we provide extensive comparisons of four multi-subject ICA approaches in combination with data reduction methods for simulated and fMRI task data. For multi-subject ICA, the data first undergo reduction at the subject and group levels using principal component analysis (PCA). Comparisons of subject-specific, spatial concatenation, and group data mean subject-level reduction strategies using PCA and probabilistic PCA (PPCA) show that computationally intensive PPCA is equivalent to PCA, and that subject-specific and group data mean subject-level PCA are preferred because of well-estimated TCs and SMs. Second, aggregate independent components are estimated using either noise-free ICA or probabilistic ICA (PICA). Third, subject-specific SMs and TCs are estimated using back-reconstruction. We compare several direct group ICA (GICA) back-reconstruction approaches (GICA1-GICA3) and an indirect back-reconstruction approach, spatio-temporal regression (STR, or dual regression). Results show the earlier group ICA (GICA1) approximates STR, however STR has contradictory assumptions and may show mixed-component artifacts in estimated SMs. Our evidence-based recommendation is to use GICA3, introduced here, with subject-specific PCA and noise-free ICA, providing the most robust and accurate estimated SMs and TCs in addition to offering an intuitive interpretation.
Copyright © 2010 Wiley Periodicals, Inc.
Figures
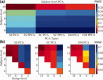
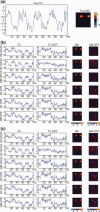
 values for subject‐level PCA/PPCA reduction for a range of components retained using three methods: subject‐specific (SS), spatial‐concatenation (SC), and group data mean (GM). (b) Mean of
values for subject‐level PCA/PPCA reduction for a range of components retained using three methods: subject‐specific (SS), spatial‐concatenation (SC), and group data mean (GM). (b) Mean of
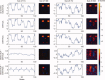
 values for total PCA reduction for a range of components retained at the subject‐level and group‐level. Smaller RMSE indicates more information retained.
values for total PCA reduction for a range of components retained at the subject‐level and group‐level. Smaller RMSE indicates more information retained.
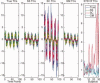


 and
and
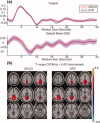
 (notation for GICA3), closer to zero is better. Solid circles are ICA and open circles are PICA.
(notation for GICA3), closer to zero is better. Solid circles are ICA and open circles are PICA.
 (notation for GICA3), closer to zero is better. Solid circles are ICA and open circles are PICA.
(notation for GICA3), closer to zero is better. Solid circles are ICA and open circles are PICA.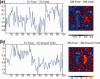


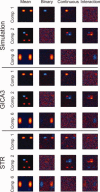
References
-
- Attias H ( 1999): Independent factor analysis. Neural Computation 11: 803–851. - PubMed
-
- Bartholomew DJ, Knott M ( 1987): Latent Variable Models and Factor Analysis. Griffin London.
-
- Basilevsky A ( 1994): Statistical Factor Analysis and Related Methods: Theory and Applications. New York: Wiley.
-
- Beckmann CF, Mackay CE, Filippini N, Smith SM ( 2009): Group comparison of resting‐state fMRI data using multi‐subject ICA and dual regression. FMRIB Centre, Dept. of Clinical Neurology, University of Oxford, Oxford, United Kingdom: Available at: http://www.humanbrainmapping.org/files/HBM2009OnsiteProgram-Final.pdf.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

