On the mechanics underlying the reservoir-excess separation in systemic arteries and their implications for pulse wave analysis
- PMID: 21165776
- PMCID: PMC3015199
- DOI: 10.1007/s10558-010-9109-9
On the mechanics underlying the reservoir-excess separation in systemic arteries and their implications for pulse wave analysis
Abstract
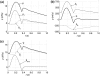
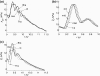
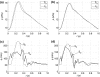
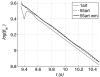
Several works have separated the pressure waveform p in systemic arteries into reservoir p(r) and excess p(exc) components, p = p(r) + p(exc), to improve pulse wave analysis, using windkessel models to calculate the reservoir pressure. However, the mechanics underlying this separation and the physical meaning of p(r) and p(exc) have not yet been established. They are studied here using the time-domain, inviscid and linear one-dimensional (1-D) equations of blood flow in elastic vessels. Solution of these equations in a distributed model of the 55 larger human arteries shows that p(r) calculated using a two-element windkessel model is space-independent and well approximated by the compliance-weighted space-average pressure of the arterial network. When arterial junctions are well-matched for the propagation of forward-travelling waves, p(r) calculated using a three-element windkessel model is space-dependent in systole and early diastole and is made of all the reflected waves originated at the terminal (peripheral) reflection sites, whereas p(exc) is the sum of the rest of the waves, which are obtained by propagating the left ventricular flow ejection without any peripheral reflection. In addition, new definitions of the reservoir and excess pressures from simultaneous pressure and flow measurements at an arbitrary location are proposed here. They provide valuable information for pulse wave analysis and overcome the limitations of the current two- and three-element windkessel models to calculate p(r).
Figures



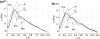
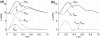

References
-
- Alastruey J. Numerical modelling of pulse wave propagation in the cardiovascular system: development, validation and clinical applications. Ph.D. thesis, Imperial College London, University of London, UK 2006.
-
- Alastruey J, Parker K, Peiró J, Sherwin S. Lumped parameter outflow models for 1-D blood flow simulations: effect on pulse waves and parameter estimation. Commun Comput Phys. 2008;4:317–36.
-
- Alastruey J, Parker K, Peiró J, Sherwin S. Analysing the pattern of pulse waves in arterial networks: a time-domain study. J Eng Math. 2009;64:331–51. doi: 10.1007/s10665-009-9275-1. - DOI
-
- Caro C, Pedley T, Schroter R, Seed W. The mechanics of the circulation. Oxford: Oxford University Press; 1978.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
