A mathematical model of the myogenic response to systolic pressure in the afferent arteriole

Abstract

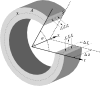
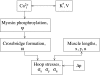
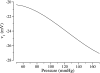
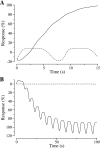
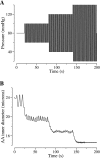
Elevations in systolic blood pressure are believed to be closely linked to the pathogenesis and progression of renal diseases. It has been hypothesized that the afferent arteriole (AA) protects the glomerulus from the damaging effects of hypertension by sensing increases in systolic blood pressure and responding with a compensatory vasoconstriction (Loutzenhiser R, Bidani A, Chilton L. Circ Res 90: 1316-1324, 2002). To investigate this hypothesis, we developed a mathematical model of the myogenic response of an AA wall, based on an arteriole model (Gonzalez-Fernandez JM, Ermentrout B. Math Biosci 119: 127-167, 1994). The model incorporates ionic transport, cell membrane potential, contraction of the AA smooth muscle cell, and the mechanics of a thick-walled cylinder. The model represents a myogenic response based on a pressure-induced shift in the voltage dependence of calcium channel openings: with increasing transmural pressure, model vessel diameter decreases; and with decreasing pressure, vessel diameter increases. Furthermore, the model myogenic mechanism includes a rate-sensitive component that yields constriction and dilation kinetics similar to behaviors observed in vitro. A parameter set is identified based on physical dimensions of an AA in a rat kidney. Model results suggest that the interaction of Ca(2+) and K(+) fluxes mediated by voltage-gated and voltage-calcium-gated channels, respectively, gives rise to periodicity in the transport of the two ions. This results in a time-periodic cytoplasmic calcium concentration, myosin light chain phosphorylation, and cross-bridge formation with the attending muscle stress. Furthermore, the model predicts myogenic responses that agree with experimental observations, most notably those which demonstrate that the renal AA constricts in response to increases in both steady and systolic blood pressures. The myogenic model captures these essential functions of the renal AA, and it may prove useful as a fundamental component in a multiscale model of the renal microvasculature suitable for investigations of the pathogenesis of hypertensive renal diseases.

Fig. 1.

Longitudinal (S) and transverse (A) sections of the vessel cylinder. x denotes the circumferential length. Coordinates r, θ, and z denote the radial, angular, and axial directions. The hoop forces f_x, f_y, and f_u are perpendicular to S.

Fig. 2.

Flow chart that illustrates the steps by which periodic oscillations in cytosolic calcium concentration (Ca_i²⁺) give rise to spontaneous vasomotion of the model afferent arteriole wall. Δp, Transmural pressure.

Fig. 6.

Average vessel inner diameter as a function of steady-state transmural pressure, with and without a myogenic response.

Fig. 3.

Steady-state voltage at which half of the channels are open (v₁) as a function of transmural pressure, as given by Eq. 10.

Fig. 4.

A: step perturbation in transmural pressure. B–F: time courses of the resulting v₁, Ca²⁺ current, intracellular free calcium concentration Ca_i, membrane potential v, and AA inner diameter.

Fig. 5.

Base-case oscillation profiles. A: oscillations in Ca²⁺ and K⁺ currents (denoted I_Ca and I_K, respectively) and membrane potential v. B: oscillations in equilibrium distribution of open Ca²⁺ and K⁺ channel states (denoted m_∞ and n_∞, respectively). C and D: oscillations in intracellular free Ca²⁺ concentration and AA inner diameter, respectively.

Fig. 7.

Average membrane potential as a function of steady-state transmural pressure, obtained for base-case membrane Ca²⁺ conductance g_Ca and for g_Ca reduced by a factor of 10.

Fig. 8.

Kinetics of AA vasoconstrictive response to pressure increase (80–160 mmHg; A) or decrease (160–80 mmHg; B). Solid line, oscillations in AA inner diameter given as percentage of maximal response; dashed line, oscillations in AA inner diameter in the absence of pressure changes.

Fig. 9.

A1: single-step pressure perturbation, followed by a period pulse train at 1 Hz. A2: similar pressure perturbations, but with a slower period pulse train at 0.05 Hz. B1 and B2: corresponding changes in AA inner diameter.

Fig. 10.

A: oscillatory pressure perturbation with amplitude (and systolic pressure) increasing by steps, while a mean constant pressure of 80 mmHg is maintained. B: corresponding AA inner diameter.