MTML-msBayes: approximate Bayesian comparative phylogeographic inference from multiple taxa and multiple loci with rate heterogeneity
- PMID: 21199577
- PMCID: PMC3031198
- DOI: 10.1186/1471-2105-12-1
MTML-msBayes: approximate Bayesian comparative phylogeographic inference from multiple taxa and multiple loci with rate heterogeneity
Abstract
Background: MTML-msBayes uses hierarchical approximate Bayesian computation (HABC) under a coalescent model to infer temporal patterns of divergence and gene flow across codistributed taxon-pairs. Under a model of multiple codistributed taxa that diverge into taxon-pairs with subsequent gene flow or isolation, one can estimate hyper-parameters that quantify the mean and variability in divergence times or test models of migration and isolation. The software uses multi-locus DNA sequence data collected from multiple taxon-pairs and allows variation across taxa in demographic parameters as well as heterogeneity in DNA mutation rates across loci. The method also allows a flexible sampling scheme: different numbers of loci of varying length can be sampled from different taxon-pairs.
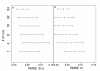
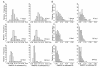
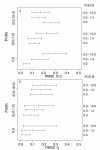
Results: Simulation tests reveal increasing power with increasing numbers of loci when attempting to distinguish temporal congruence from incongruence in divergence times across taxon-pairs. These results are robust to DNA mutation rate heterogeneity. Estimating mean divergence times and testing simultaneous divergence was less accurate with migration, but improved if one specified the correct migration model. Simulation validation tests demonstrated that one can detect the correct migration or isolation model with high probability, and that this HABC model testing procedure was greatly improved by incorporating a summary statistic originally developed for this task (Wakeley's ΨW). The method is applied to an empirical data set of three Australian avian taxon-pairs and a result of simultaneous divergence with some subsequent gene flow is inferred.
Conclusions: To retain flexibility and compatibility with existing bioinformatics tools, MTML-msBayes is a pipeline software package consisting of Perl, C and R programs that are executed via the command line. Source code and binaries are available for download at http://msbayes.sourceforge.net/ under an open source license (GNU Public License).
Figures
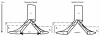



Similar articles
-
msBayes: pipeline for testing comparative phylogeographic histories using hierarchical approximate Bayesian computation.BMC Bioinformatics. 2007 Jul 26;8:268. doi: 10.1186/1471-2105-8-268. BMC Bioinformatics. 2007. PMID: 17655753 Free PMC article.
-
Testing comparative phylogeographic models of marine vicariance and dispersal using a hierarchical Bayesian approach.BMC Evol Biol. 2008 Nov 27;8:322. doi: 10.1186/1471-2148-8-322. BMC Evol Biol. 2008. PMID: 19038027 Free PMC article.
-
Strategies for improving approximate Bayesian computation tests for synchronous diversification.BMC Evol Biol. 2017 Aug 24;17(1):203. doi: 10.1186/s12862-017-1052-6. BMC Evol Biol. 2017. PMID: 28836959 Free PMC article.
-
Perspective: gene divergence, population divergence, and the variance in coalescence time in phylogeographic studies.Evolution. 2000 Dec;54(6):1839-54. doi: 10.1111/j.0014-3820.2000.tb01231.x. Evolution. 2000. PMID: 11209764 Review.
-
GADMA2: more efficient and flexible demographic inference from genetic data.Gigascience. 2022 Dec 28;12:giad059. doi: 10.1093/gigascience/giad059. Epub 2023 Aug 23. Gigascience. 2022. PMID: 37609916 Free PMC article. Review.
Cited by
-
In-Situ pH-Sensitive Fibers via the Anchoring of Bromothymol Blue on Cellulose Grafted with Hydroxypropyltriethylamine Groups via Adsorption.Polymers (Basel). 2018 Jun 27;10(7):709. doi: 10.3390/polym10070709. Polymers (Basel). 2018. PMID: 30960634 Free PMC article.
-
Comparative phylogeographic analyses illustrate the complex evolutionary history of threatened cloud forests of northern Mesoamerica.PLoS One. 2013;8(2):e56283. doi: 10.1371/journal.pone.0056283. Epub 2013 Feb 7. PLoS One. 2013. PMID: 23409165 Free PMC article.
-
Habitat suitability mapping and landscape connectivity analysis to predict African swine fever spread in wild boar populations: A focus on Northern Italy.PLoS One. 2025 Jan 30;20(1):e0317577. doi: 10.1371/journal.pone.0317577. eCollection 2025. PLoS One. 2025. PMID: 39883672 Free PMC article.
-
A novel TP53 tandem duplication in a child with Li-Fraumeni syndrome.Cold Spring Harb Mol Case Stud. 2022 Apr 28;8(3):a006181. doi: 10.1101/mcs.a006181. Print 2022 Apr. Cold Spring Harb Mol Case Stud. 2022. PMID: 35232817 Free PMC article.
-
Full Bayesian Comparative Phylogeography from Genomic Data.Syst Biol. 2019 May 1;68(3):371-395. doi: 10.1093/sysbio/syy063. Syst Biol. 2019. PMID: 30239868 Free PMC article.
References
-
- Bermingham E, Moritz C. Comparative phylogeography: concepts and applications. Mol Ecol. 1998;7:367–369. doi: 10.1046/j.1365-294x.1998.00424.x. - DOI
-
- Arbogast BS, Kenagy GJ. Comparative phylogeography as an integrative approach to historical biogeography. J Biogeogr. 2001;28:819–825. doi: 10.1046/j.1365-2699.2001.00594.x. - DOI
-
- Coyne JA, Orr HA. Speciation. Sunderland, MA: Sinauer Associates Inc; 2004.
-
- Avise JC. Phylogeography: The history and formation of species. Cambridge: Harvard University Press; 2000.
-
- Hubbell SP. The Unified Neutral Theory of Biodiversity and Biogeography. Princeton, NJ: Princeton University Press; 2001.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

