Diffeomorphic registration using geodesic shooting and Gauss-Newton optimisation
- PMID: 21216294
- PMCID: PMC3221052
- DOI: 10.1016/j.neuroimage.2010.12.049
Diffeomorphic registration using geodesic shooting and Gauss-Newton optimisation
Abstract
This paper presents a nonlinear image registration algorithm based on the setting of Large Deformation Diffeomorphic Metric Mapping (LDDMM), but with a more efficient optimisation scheme--both in terms of memory required and the number of iterations required to reach convergence. Rather than perform a variational optimisation on a series of velocity fields, the algorithm is formulated to use a geodesic shooting procedure, so that only an initial velocity is estimated. A Gauss-Newton optimisation strategy is used to achieve faster convergence. The algorithm was evaluated using freely available manually labelled datasets, and found to compare favourably with other inter-subject registration algorithms evaluated using the same data.
Copyright © 2011 Elsevier Inc. All rights reserved.
Figures


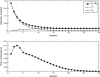



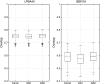
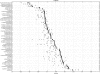
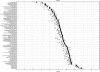
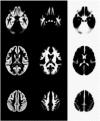


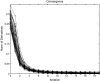

References
-
- Andersson J.L.R., Jenkinson M., Smith S.M. FMRIB Analysis Group Technical Reports: TR07JA02. 2007. Non-linear registration, aka spatial normalisation.
-
- Ardekani B.A., Braun M., Hutton B.F., Kanno I., Iida H. A fully automatic multimodality image registration algorithm. Journal of computer assisted tomography. 1995;190(4):615. - PubMed
-
- Arsigny V., Commowick O., Pennec X., Ayache N. Medical Image Computing and Computer-Assisted Intervention — MICCAI 2006. 2006. A Log-Euclidean framework for statistics on diffeomorphisms; pp. 924–931. - PubMed
-
- Arsigny V., Commowick O., Ayache N., Pennec X. A fast and log-Euclidean polyaffine framework for locally linear registration. Journal of Mathematical Imaging and Vision. 2009;330(2):222–238.
-
- Ashburner J. A fast diffeomorphic image registration algorithm. Neuroimage. 2007;380(1):95–113. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

