Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry
- PMID: 21224418
- PMCID: PMC3033264
- DOI: 10.1073/pnas.1008695108
Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry
Abstract
Micelles are the simplest example of self-assembly found in nature. As many other colloids, they can self-assemble in aqueous solution to form ordered periodic structures. These structures so far all exhibited classical crystallographic symmetries. Here we report that micelles in solution can self-assemble into quasicrystalline phases. We observe phases with 12-fold and 18-fold diffraction symmetry. Colloidal water-based quasicrystals are physically and chemically very simple systems. Macroscopic monodomain samples of centimeter dimension can be easily prepared. Phase transitions between the fcc phase and the two quasicrystalline phases can be easily followed in situ by time-resolved diffraction experiments. The discovery of quasicrystalline colloidal solutions advances the theoretical understanding of quasicrystals considerably, as for these systems the stability of quasicrystalline states has been theoretically predicted for the concentration and temperature range, where they are experimentally observed. Also for the use of quasicrystals in advanced materials this discovery is of particular importance, as it opens the route to quasicrystalline photonic band gap materials via established water-based colloidal self-assembly techniques.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


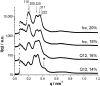
 ). The scattering curves at lower concentrations are characterized by a suppression of the intensity of the 110 reflection and the development of a peak at q∗ = 0.45 nm-1, which for the dodecagonal structure corresponds to the 20100 reflection.
). The scattering curves at lower concentrations are characterized by a suppression of the intensity of the 110 reflection and the development of a peak at q∗ = 0.45 nm-1, which for the dodecagonal structure corresponds to the 20100 reflection.

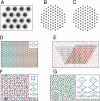
References
-
- Förster S, Plantenberg T. From self-organizing polymers to nanohybrid and biomaterials. Angew Chem Int Edit. 2002;41:688–714. - PubMed
-
- Förster S, et al. Order causes secondary Bragg-peaks in soft materials. Nat Mater. 2007;6:888–893. - PubMed
-
- Chaikin PM, Lubensky TC. Principles of Condensed Matter Physics. Cambridge, UK: Cambridge Univ Press; 1995.
-
- Navailles L, Barois P, Nguyen HT. X-Ray measurements of the twist grain boundary angle in the liquid crystal analog of the Abrikosov phase. Phys Rev Lett. 1993;71:545–548. - PubMed
-
- Barois P, et al. Synchrotron X-ray study of the q-fold quasicrystalline symmetry of the smectic C twist grain boundary phase (TGBc) Eur Phys J B. 1999;11:455–462.
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

