A theoretical analysis of filament length fluctuations in actin and other polymers
- PMID: 21234568
- PMCID: PMC3099255
- DOI: 10.1007/s00285-010-0400-6
A theoretical analysis of filament length fluctuations in actin and other polymers
Abstract
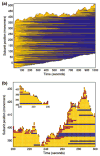
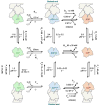
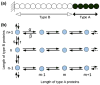
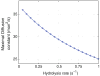
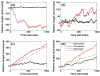
Control of the structure and dynamics of the actin cytoskeleton is essential for cell motility and for maintaining the structural integrity of cells. Central to understanding the control of these features is an understanding of the dynamics of actin filaments, first as isolated filaments, then as integrated networks, and finally as networks containing higher-order structures such as bundles, stress fibers and acto-myosin complexes. It is known experimentally that single filaments can exhibit large fluctuations, but a detailed understanding of the transient dynamics involved is still lacking. Here we first study stochastic models of a general system involving two-monomer types that can be analyzed completely, and then we report stochastic simulations on the complete actin model with three monomer types. We systematically examine the transient behavior of filament length dynamics so as to gain a better understanding of the time scales involved in reaching a steady state. We predict the lifetime of a cap of one monomer type and obtain the mean and variance of the survival time of a cap at the filament end, which together determine the filament length fluctuations.
© Springer-Verlag 2011
Figures
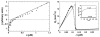
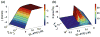
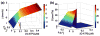



References
-
- Abramowitz M, Stegun I. Handbook of mathematical functions. 1965.
-
- Bugyi B, Carlier MF. Control of actin filament treadmilling in cell motility. Annu Rev Biophys. 2010;39:449–470. - PubMed
-
- Carlier MF, Pantaloni D, Korn ED. The effects of Mg2+ at the high-affinity and low-affinity sites on the polymerization of actin and associated ATP hydrolysis. J Biol Chem. 1986;261:10785–10792. - PubMed
-
- Carlsson AE. Model of reduction of actin polymerization forces by ATP hydrolysis. Phys Biol. 2008;5(3):1–9. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

