The Future of Indirect Evidence

Abstract

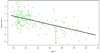
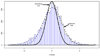
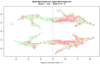
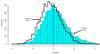
Familiar statistical tests and estimates are obtained by the direct observation of cases of interest: a clinical trial of a new drug, for instance, will compare the drug's effects on a relevant set of patients and controls. Sometimes, though, indirect evidence may be temptingly available, perhaps the results of previous trials on closely related drugs. Very roughly speaking, the difference between direct and indirect statistical evidence marks the boundary between frequentist and Bayesian thinking. Twentieth-century statistical practice focused heavily on direct evidence, on the grounds of superior objectivity. Now, however, new scientific devices such as microarrays routinely produce enormous data sets involving thousands of related situations, where indirect evidence seems too important to ignore. Empirical Bayes methodology offers an attractive direct/indirect compromise. There is already some evidence of a shift toward a less rigid standard of statistical objectivity that allows better use of indirect evidence. This article is basically the text of a recent talk featuring some examples from current practice, with a little bit of futuristic speculation.

Figure 1

Roberto Clemente’s batting averages over the 1970 baseball season (partially simulated). After 45 tries he had 18 hits for a batting average of 18/45 = .400; his average in the remainder of the season was 127/367 = .346.

Figure 2

Kidney function plotted versus age for 157 healthy volunteers from the nephrology laboratory of Dr. Brian Myers. The least squares regression line has a strong downward slope. A new donor age 55 has appeared, and we need to predict his kidney score.

Figure 3

Histogram of N = 6033 z-values from the prostate cancer study compared with the theoretical null density that would apply if all the genes were uninteresting. Hash marks indicate the 49 z-values exceeding 3.0.

Figure 4

Close-up of right tail of the prostate data z-value histogram; 49 z_i’s exceed 3.0, compared to an expected number 8.14 if all genes were null (4).

Figure 5

Histogram of z-values for N = 7128 genes in a microarray study comparing two types of leukemia. The N(0, 1) theoretical null is much narrower than the histogram center; a normal fit to the central histogram height gives empirical null N(.09, 1.68²). Both curves have been scaled by their respective estimates of p₀ in (7).

Figure 6

DTI study z-values comparing 6 dyslexic children with 6 normal controls, at N = 15443 voxels; shown is horizontal section of 848 voxels; x indicates distance from back of brain (left) to front (right). The vertical line at x = 50 divides the brain into back and front halves.

Figure 7

Separate histograms for z_i’s from the front and back halves of the brain, DTI study. The heavy right tail of the front-half data yields 281 significant voxels in an Fdr test, control level q = .10.

Figure 8

z-values for the 15,443 voxels plotted versus their distance from the back of the brain. A disturbing wave pattern is evident, cresting near x = 64. Most of the 281 significant voxels in Figure 7 come from this crest.

Figure 9

Empirical Bayes effect size estimate Ê{μ|z} (16), prostate data of Figure 3. Dots indicate the top 10 genes, those with the greatest values of |z_i| The top gene, i = 610, has z_i = 5.29 and estimated effect size 4.11.