Extended Fujita approach to the molecular weight distribution of polysaccharides and other polymeric systems

Abstract

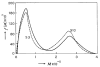
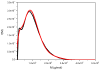
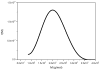
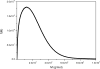
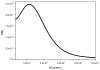
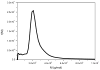
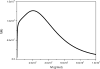
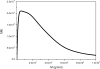
In 1962 H. Fujita (H. Fujita, Mathematical Theory of Sedimentation Analysis, Academic Press, New York, 1962) examined the possibility of transforming a quasi-continuous distribution g(s) of sedimentation coefficient s into a distribution f(M) of molecular weight M for linear polymers using the relation f(M)=g(s)·(ds/dM) and showed that this could be done if information about the relation between s and M is available from other sources. Fujita provided the transformation based on the scaling relation s=κ(s)M(0.5), where κ(s) is taken as a constant for that particular polymer and the exponent 0.5 essentially corresponds to a randomly coiled polymer under ideal conditions. This method has been successfully applied to mucus glycoproteins (S.E. Harding, Adv. Carbohyd. Chem. Biochem. 47 (1989) 345-381). We now describe an extension of the method to general conformation types via the scaling relation s=κM(b), where b=0.4-0.5 for a coil, ∼0.15-0.2 for a rod and ∼0.67 for a sphere. We give examples of distributions f(M) versus M obtained for polysaccharides from SEDFIT derived least squares g(s) versus s profiles (P. Schuck, Biophys. J. 78 (2000) 1606-1619) and the analytical derivative for ds/dM performed with Microcal ORIGIN. We also describe a more direct route from a direct numerical solution of the integral equation describing the molecular weight distribution problem. Both routes give identical distributions although the latter offers the advantage of being incorporated completely within SEDFIT. The method currently assumes that solutions behave ideally: sedimentation velocity has the major advantage over sedimentation equilibrium in that concentrations less than 0.2mg/ml can be employed, and for many systems non-ideality effects can be reasonably ignored. For large, non-globular polymer systems, diffusive contributions are also likely to be small.

Figure 1

Sedimentation equilibrium of a polydisperse polymer system: Rayleigh interference fringes for a bronchial mucus glycoprotein (BM-GRE, M_w ~ 6.0×10⁶ g/mol). A loading concentration of ~0.2 mg/ml in a Beckman Model E analytical ultracentrifuge (rotor speed 1967rpm) and a cell of 30mm optical path length was used. The direction of sedimentation is from left to right. Note the very steep rising fringes at the cell base and yet there is still a finite curvature at the air-solution meniscus [10].

Figure 2

Sedimentation velocity of a polydisperse polymer system: A subset of radial displacement profiles displayed in SEDFIT obtained from Rayleigh interference fringes (scanned every 2 min) for a low methoxy pectin (M_w ~ 380,000 g/mol). A loading concentration of 0.15 mg/ml in a Beckman XL-I analytical ultracentrifuge (rotor speed 45000 rpm) and a cell of 12mm optical path length was used. The direction of sedimentation is from left to right.

Figure 3

Fujita’s plot [1] of sedimentation coefficient distribution for a 50:50 mixture of two polystyrene samples S3 and S10 in cyclohexane obtained using Eqs. (7–12). The dashed line represents the predicted distribution for the mixture based on the individually obtained distributions for S3 and S10. [Permission being sort from Elsevier].

Figure 4

Molecular weight distribution, f(M) vs M, for konjac glucomannan obtained from the ls-g(s) versus distribution and analytical derivative (black line) and direct or full numerical (red line) procedures. Loading concentration c_o ~ 0.25 mg/ml. κ_s = 0.044 and b = 0.32. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C in 0.1 M pH 6.8 phosphate buffer. M_w = 840000 g/mol.

Figure 5

Molecular weight distribution f(M) vs M for pullulan P200. Loading concentration c_o ~ 0.1 mg/ml. κ_s = 0.025 and b = 0.46. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C in 0.1 M pH 6.8 phosphate buffer. M_w = 197000 g/mol.

Figure 6

Molecular weight distributions f(M) versus M for (a) high methoxyl pectin and (b) low methoxy pectin. Samples were centrifuged at 45000 rpm at a temperature of 20.0 °C in 0.1 M sodium chloride. For both cases, κ_s = 0.017 and b = 0.39. (a) Loading concentration c_o ~ 0.20 mg/ml. M_w = 150 000 (g/mol) (b) Loading concentration c_o ~ 0.15 mg/ml. M_w = 230 000 g/mol.

Figure 6

Molecular weight distributions f(M) versus M for (a) high methoxyl pectin and (b) low methoxy pectin. Samples were centrifuged at 45000 rpm at a temperature of 20.0 °C in 0.1 M sodium chloride. For both cases, κ_s = 0.017 and b = 0.39. (a) Loading concentration c_o ~ 0.20 mg/ml. M_w = 150 000 (g/mol) (b) Loading concentration c_o ~ 0.15 mg/ml. M_w = 230 000 g/mol.

Figure 7

Molecular weight distribution f(M) vs M for a commercial alginate. Loading concentration c_o ~ 0.2 mg/ml. κ_s = 0.052 and b = 0.33. Sample was centrifuged at 45 000 rpm at a temperature of 20.0 °C in 0.1 M pH 6.8 phosphate buffer. M_w = 140 000 g/mol. NB. The limit for reliable sedimentation coefficient values is >0.5S.

Figure 8

Molecular weight distribution f(M) vs M for xanthan. Loading concentration c_o ~ 0.2 mg/ml in 0.1 M pH 6.8 phosphate buffer. κ_s = 0.197 and b = 0.26. Rotor speed = 45000 rpm at a temperature of 20.0 °C. M_w = 2.6 × 10⁶ g/mol.

Figure 9

Molecular weight distribution f(M) vs M for chitosan of degree of acetylation ~20%. Loading concentration c_o ~ 0.25 mg/ml in 0.2 M pH 4.3 acetate buffer. κ_s = 0.10 and b = 0.24. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C. M_w = 210 000 g/mol. NB. The distributions shown extend to higher molar masses.

Figure 10

Molecular weight distribution, f(M) vs M for a mucin glycopeptides HMG Hug from human gastric mucin. Loading concentration c_o ~ 0.3 mg/ml in 0.1 M pH 6.8 phosphate buffer. κ_s = 0.008 and b = 0.50. Sample was centrifuged at 45000 rpm at a temperature of 20.0 °C. NB The distributions shown extend to higher molar masses.

Figure 11

Molecular weight distribution for a large glycoconjugate construct of a protein and bacterial polysaccharide. Loading concentration c_o ~ 0.3 mg/ml in 0.1 M pH 6.8 phosphate buffer.. The distributions for two different selections of the power law coefficient b are shown. The sample was centrifuged at 7000 rpm at a temperature of 20.0°C.