A general approach for population games with application to vaccination
- PMID: 21277314
- PMCID: PMC3063328
- DOI: 10.1016/j.mbs.2011.01.003
A general approach for population games with application to vaccination
Abstract
Reconciling the interests of individuals with the interests of communities is a major challenge in designing and implementing health policies. In this paper, we present a technique based on a combination of mechanistic population-scale models, Markov decision process theory and game theory that facilitates the evaluation of game theoretic decisions at both individual and community scales. To illustrate our technique, we provide solutions to several variants of the simple vaccination game including imperfect vaccine efficacy and differential waning of natural and vaccine immunity. In addition, we show how path-integral approaches can be applied to the study of models in which strategies are fixed waiting times rather than exponential random variables. These methods can be applied to a wide variety of decision problems with population-dynamic feedbacks.
Copyright © 2011 Elsevier Inc. All rights reserved.
Figures
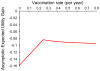


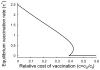
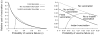

References
-
- Kenneth J. Public Investment, the Rate of Return, and Optimal Fiscal Policy. Johns Hopkins Press; Baltimore, MD: 1970. Arrow and Mordecai Kurz.
-
- Barrett S. Global disease eradication. Journal of the European Economic Association. 2003;1(2):591–600.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

