Control of the mitotic cleavage plane by local epithelial topology
- PMID: 21295702
- PMCID: PMC3491649
- DOI: 10.1016/j.cell.2010.12.035
Control of the mitotic cleavage plane by local epithelial topology
Abstract
For nearly 150 years, it has been recognized that cell shape strongly influences the orientation of the mitotic cleavage plane (e.g., Hofmeister, 1863). However, we still understand little about the complex interplay between cell shape and cleavage-plane orientation in epithelia, where polygonal cell geometries emerge from multiple factors, including cell packing, cell growth, and cell division itself. Here, using mechanical simulations, we show that the polygonal shapes of individual cells can systematically bias the long-axis orientations of their adjacent mitotic neighbors. Strikingly, analyses of both animal epithelia and plant epidermis confirm a robust and nearly identical correlation between local cell topology and cleavage-plane orientation in vivo. Using simple mathematics, we show that this effect derives from fundamental packing constraints. Our results suggest that local epithelial topology is a key determinant of cleavage-plane orientation, and that cleavage-plane bias may be a widespread property of polygonal cell sheets in plants and animals.
Copyright © 2011 Elsevier Inc. All rights reserved.
Figures




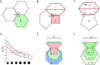
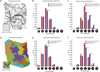
Comment in
-
Getting cells and tissues into shape.Cell. 2011 Feb 4;144(3):325-6. doi: 10.1016/j.cell.2011.01.022. Cell. 2011. PMID: 21295695
References
-
- Aegerter-Wilmsen T, Smith AC, Christen AJ, Aegerter CM, Hafen E, Basler K. Exploring the effects of mechanical feedback on epithelial topology. Development. 2010;137:499–506. - PubMed
-
- Baena-Lopez LA, Baonza A, Garcia-Bellido A. The orientation of cell divisions determines the shape of Drosophila organs. Curr Biol. 2005;15:1640–1644. - PubMed
-
- Black SD, Vincent JP. The first cleavage plane and the embryonic axis are determined by separate mechanisms in Xenopus laevis. II. Experimental dissociation by lateral compression of the egg. Dev Biol. 1988;128:65–71. - PubMed
-
- Brodland GW, Veldhuis JH. Computer simulations of mitosis and interdependencies between mitosis orientation, cell shape and epithelia reshaping. J Biomech. 2002;35:673–681. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

