The role of additive neurogenesis and synaptic plasticity in a hippocampal memory model with grid-cell like input
- PMID: 21298080
- PMCID: PMC3029236
- DOI: 10.1371/journal.pcbi.1001063
The role of additive neurogenesis and synaptic plasticity in a hippocampal memory model with grid-cell like input
Abstract
Recently, we presented a study of adult neurogenesis in a simplified hippocampal memory model. The network was required to encode and decode memory patterns despite changing input statistics. We showed that additive neurogenesis was a more effective adaptation strategy compared to neuronal turnover and conventional synaptic plasticity as it allowed the network to respond to changes in the input statistics while preserving representations of earlier environments. Here we extend our model to include realistic, spatially driven input firing patterns in the form of grid cells in the entorhinal cortex. We compare network performance across a sequence of spatial environments using three distinct adaptation strategies: conventional synaptic plasticity, where the network is of fixed size but the connectivity is plastic; neuronal turnover, where the network is of fixed size but units in the network may die and be replaced; and additive neurogenesis, where the network starts out with fewer initial units but grows over time. We confirm that additive neurogenesis is a superior adaptation strategy when using realistic, spatially structured input patterns. We then show that a more biologically plausible neurogenesis rule that incorporates cell death and enhanced plasticity of new granule cells has an overall performance significantly better than any one of the three individual strategies operating alone. This adaptation rule can be tailored to maximise performance of the network when operating as either a short- or long-term memory store. We also examine the time course of adult neurogenesis over the lifetime of an animal raised under different hypothetical rearing conditions. These growth profiles have several distinct features that form a theoretical prediction that could be tested experimentally. Finally, we show that place cells can emerge and refine in a realistic manner in our model as a direct result of the sparsification performed by the dentate gyrus layer.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

 -dimensional EC input pattern,
-dimensional EC input pattern,  , is generated from a phenomenological model of grid cell firing and encoded into a binary
, is generated from a phenomenological model of grid cell firing and encoded into a binary  -dimensional DG representation,
-dimensional DG representation,  . The encoded pattern is stored and later retrieved, then inverted to reproduce a continuous approximation to the original pattern,
. The encoded pattern is stored and later retrieved, then inverted to reproduce a continuous approximation to the original pattern,  . The networks we simulate in the results section have
. The networks we simulate in the results section have  units in the input layer and up to
units in the input layer and up to  units in the hidden layer.
units in the hidden layer.
 . Firing rates range from zero Hertz (white) to twelve Hertz (black). The dashed lines indicate the “centre line” of each grid which passes through the grid origin. The grids have different origins as well as vertex spacings and field sizes, but similar orientations. Right panels: The same two grids after entry to environment
. Firing rates range from zero Hertz (white) to twelve Hertz (black). The dashed lines indicate the “centre line” of each grid which passes through the grid origin. The grids have different origins as well as vertex spacings and field sizes, but similar orientations. Right panels: The same two grids after entry to environment  . The grids have undergone a coherent rotation of grid orientation and independent random shifts in grid origin. The dashed lines show the new grid centre lines in environment
. The grids have undergone a coherent rotation of grid orientation and independent random shifts in grid origin. The dashed lines show the new grid centre lines in environment  superimposed on the (unrotated) centre line from the previous environment
superimposed on the (unrotated) centre line from the previous environment  , shown as a dotted line.
, shown as a dotted line.
 DG units. The recoding error of the fixed network (upper solid line) is a measure of how well a completely generic network deals with the statistics of the spatially driven input we have used. We expect that any adaptation strategy would produce at least this level of recoding accuracy. Right panel: Evolution of the recoding error (solid line) and the retrieval error (dashed line) as a function of environment number for a network that uses a neural gas-like plasticity algorithm with a recoding error threshold of
DG units. The recoding error of the fixed network (upper solid line) is a measure of how well a completely generic network deals with the statistics of the spatially driven input we have used. We expect that any adaptation strategy would produce at least this level of recoding accuracy. Right panel: Evolution of the recoding error (solid line) and the retrieval error (dashed line) as a function of environment number for a network that uses a neural gas-like plasticity algorithm with a recoding error threshold of  . In all subsequent plots we conform to the convention of plotting recoding errors with a solid line and retrieval errors with a dashed line. The errors lie in the range
. In all subsequent plots we conform to the convention of plotting recoding errors with a solid line and retrieval errors with a dashed line. The errors lie in the range  to
to  which we also adopt as our standard vertical scale. Conventional plasticity successfully reduces the recoding error in each environment to the target value but only at the expense of increasing the retrieval error for previously stored memory patterns.
which we also adopt as our standard vertical scale. Conventional plasticity successfully reduces the recoding error in each environment to the target value but only at the expense of increasing the retrieval error for previously stored memory patterns.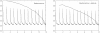
 but only at the expense of increasing the retrieval error for previously stored memory patterns. Right panel: Adding conventional plasticity improves network performance but does not qualitatively change this result.
but only at the expense of increasing the retrieval error for previously stored memory patterns. Right panel: Adding conventional plasticity improves network performance but does not qualitatively change this result.

 but from the sixth environment onwards the network starts to run out of units to add and the network can no longer achieve this level of performance. The retrieval error for previously stored memory patterns is identical to the recoding error when those patterns were stored, as the internal structure of those parts of the network used to originally encode those patterns does not change over time. Inset: A plot of a single simulation shows how this breakdown of adaptation occurs in a step-like manner when the network runs out of units to add. The gradual degradation in performance shown in the main plot is a result of averaging
but from the sixth environment onwards the network starts to run out of units to add and the network can no longer achieve this level of performance. The retrieval error for previously stored memory patterns is identical to the recoding error when those patterns were stored, as the internal structure of those parts of the network used to originally encode those patterns does not change over time. Inset: A plot of a single simulation shows how this breakdown of adaptation occurs in a step-like manner when the network runs out of units to add. The gradual degradation in performance shown in the main plot is a result of averaging  simulations, each of which breaks down at a different point in time. Right panel: Plasticity allows the network to make better use of the units it grows with the result that the network can, on average, deal fairly well with all twelve environments.
simulations, each of which breaks down at a different point in time. Right panel: Plasticity allows the network to make better use of the units it grows with the result that the network can, on average, deal fairly well with all twelve environments.
 for all twelve environments but once again suffers from an increased retrieval error. Right panel: Adding plasticity improves network performance considerably resulting in a network that can deal with all twelve environments while producing a retrieval error that is consistently lower than either conventional plasticity or neuronal turnover algorithms operating alone.
for all twelve environments but once again suffers from an increased retrieval error. Right panel: Adding plasticity improves network performance considerably resulting in a network that can deal with all twelve environments while producing a retrieval error that is consistently lower than either conventional plasticity or neuronal turnover algorithms operating alone.
 for all twelve environments. The retrieval error is the same as the recoding error for the three most recent environments then increases sharply for temporally more distant environments. Right panel: Adding plasticity improves network performance considerably. The result is a network that can deal with all twelve environments while at the same time having a retrieval error that is lower than either conventional plasticity or neuronal turnover algorithms operating alone.
for all twelve environments. The retrieval error is the same as the recoding error for the three most recent environments then increases sharply for temporally more distant environments. Right panel: Adding plasticity improves network performance considerably. The result is a network that can deal with all twelve environments while at the same time having a retrieval error that is lower than either conventional plasticity or neuronal turnover algorithms operating alone.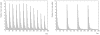
 units) is lower compared to the mean overall level of growth for twelve environments (
units) is lower compared to the mean overall level of growth for twelve environments ( units).
units).
 ,
,  ,
,  and
and  days, from left to right). Left column: After
days, from left to right). Left column: After  day in the new environment each DG cell us activated by a large area of the spatial environment. Middle left column: After
day in the new environment each DG cell us activated by a large area of the spatial environment. Middle left column: After  days a degree of refinement has occurred and the place fields have become more restricted. Middle right column: After
days a degree of refinement has occurred and the place fields have become more restricted. Middle right column: After  days further refinement leads to activation patterns that resemble place cells in the DG. Right column: After
days further refinement leads to activation patterns that resemble place cells in the DG. Right column: After  days the final response of the cells are very similar to experimentally observed place cells with one main place field and occasionally some scattered areas of secondary activation. The network uses an additive neurogenesis with plasticity algorithm, but results are qualitatively the same for any of the four variations of neurogenesis we explored in the results section.
days the final response of the cells are very similar to experimentally observed place cells with one main place field and occasionally some scattered areas of secondary activation. The network uses an additive neurogenesis with plasticity algorithm, but results are qualitatively the same for any of the four variations of neurogenesis we explored in the results section.References
-
- Bayer S. Neuron production in the hippocampus and olfactory bulb of the adult rat brain: addition or replacement? Ann N Y Acad Sci. 1985;457:163–172. - PubMed
-
- Kempermann G, Gast D, Kronenberg G, Yamaguchi M, Gage F. Early determination and long-term persistence of adult-generated new neurons in the hippocampus of mice. Development. 2003;130:391–399. - PubMed
-
- Imayoshi I, Sakamoto M, Ohtsuka T, Takao K, Miyakawa T, et al. Roles of continuous neurogenesis in the structural and functional integrity of the adult forebrain. Nat Neurosci. 2008;11:1153–1161. - PubMed
-
- Altman J, Das G. Autoradiographic and histological evidence of postnatal hippocampal neurogenesis in rats. J Comp Neurol. 1965;124:319–335. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

