3D Winding Number: Theory and Application to Medical Imaging

Abstract

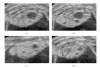
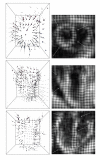
We develop a new formulation, mathematically elegant, to detect critical points of 3D scalar images. It is based on a topological number, which is the generalization to three dimensions of the 2D winding number. We illustrate our method by considering three different biomedical applications, namely, detection and counting of ovarian follicles and neuronal cells and estimation of cardiac motion from tagged MR images. Qualitative and quantitative evaluation emphasizes the reliability of the results.

Figure 1

Critical point refinement. (a) A continuum Gaussian signal in 1 dimension and the corresponding sampled signal. The sampled signal shows maxima at two nearby positions (points in red), which are at different locations from the real maximum (point in green). (b) Rasterized version of a 2-dimensional Gaussian signal. Red points are the retrieved maxima, whereas the green point is the true maximum obtained after the refinement.

Figure 2

Follicle detection. The red dots highlight the detected minima. (a) The image shows detected minima at scale s = 2. The image is very noisy, and the algorithm detects also the minima corresponding to noisy grains (false positives). (b) The image shows minima detected at scale s = 9. The arrow shows a minimum detected outside the ovarian tissue (false positive), whereas the red dot inside the ovarian tissue corresponds to the center of a follicle. (c) In this image, the false positive outside the ovarian boundaries has been filtered out.

Figure 3

Follicle detection. 2D slices of the 3D ultrasound image smoothed data set corresponding to one of the patients. Lighter areas display the ovary; dark circular blobs are the follicles. Red dots indicate retrieved local minima in 3D at scale s = 9 voxels.

Figure 4

Cerebellum cell counting. (a) A slice of stack 1. (b) A slice of stack 2. Red dots indicate neurons retrieved by the algorithm.

Figure 5

Cardiac tagged MR images, frame 3. Rows 1 and 2 from left to right: Short axis view with horizontal tags, 2 long axis views with vertical and horizontal tags, respectively. Row 3: Combination of the image planes. Row 4 displays the outcome of the combination of image planes. The images exhibit a chessboard pattern.

Figure 6

(a) The image shows a 2-dimensional slice of the 3-dimensional artificial phantom. (b) and (c) The images display the vector field of two successive frames of the phantom.

Figure 7

Three-dimensional velocity flow field of one frame of the left ventricle in phase of contraction (column 1) under 3 different views and the correspondent cross-sections of the cardiac image volume (column 2). In column 2, the left ventricle is highlighted by white arrows. Row 1 displays the short axis view, whereas rows 2 and 3 show the 2 long axis views. The retrieved 3-dimensional vectors illustrate with accuracy the cardiac motion behavior and overcome shortcomings typical of the 2-dimensional optic flow methods, such as through-plane motion detection.