Accurate measurement of brain changes in longitudinal MRI scans using tensor-based morphometry
- PMID: 21320612
- PMCID: PMC3394184
- DOI: 10.1016/j.neuroimage.2011.01.079
Accurate measurement of brain changes in longitudinal MRI scans using tensor-based morphometry
Abstract
This paper responds to Thompson and Holland (2011), who challenged our tensor-based morphometry (TBM) method for estimating rates of brain changes in serial MRI from 431 subjects scanned every 6 months, for 2 years. Thompson and Holland noted an unexplained jump in our atrophy rate estimates: an offset between 0 and 6 months that may bias clinical trial power calculations. We identified why this jump occurs and propose a solution. By enforcing inverse-consistency in our TBM method, the offset dropped from 1.4% to 0.28%, giving plausible anatomical trajectories. Transitivity error accounted for the minimal remaining offset. Drug trial sample size estimates with the revised TBM-derived metrics are highly competitive with other methods, though higher than previously reported sample size estimates by a factor of 1.6 to 2.4. Importantly, estimates are far below those given in the critique. To demonstrate a 25% slowing of atrophic rates with 80% power, 62 AD and 129 MCI subjects would be required for a 2-year trial, and 91 AD and 192 MCI subjects for a 1-year trial.
Copyright © 2011 Elsevier Inc. All rights reserved.
Figures
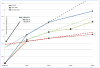
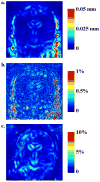

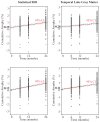
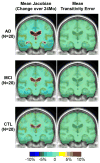
Comment on
-
Bias in tensor based morphometry Stat-ROI measures may result in unrealistic power estimates.Neuroimage. 2011 Jul 1;57(1):1-4. doi: 10.1016/j.neuroimage.2010.11.092. Epub 2011 Feb 22. Neuroimage. 2011. PMID: 21349340 Free PMC article.
References
-
- Ashburner J. A fast diffeomorphic image registration algorithm. Neuroimage. 2007;38(1):95–113. 15. - PubMed
-
- Braak H, Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol; (Berl) 1991;82(4):239–59. - PubMed
-
- Cachier P, Rey D. Symmetrization of the Non-Rigid Registration Problem using Invertion-Invariant Energies: Application to Multiple Sclerosis. Proc of MICCAI 2000. 2000:472–481. October 2000.
-
- Carlson NE, Moore MM, Dame A, Howieson D, Silbert LC, Quinn JF, Kaye JA. Trajectories of brain loss in aging and the development of cognitive impairment. Neurology. 2008;70:828–33. - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources

