A random-effects model for group-level analysis of diffuse optical brain imaging
- PMID: 21326631
- PMCID: PMC3028484
- DOI: 10.1364/BOE.2.000001
A random-effects model for group-level analysis of diffuse optical brain imaging
Abstract
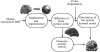
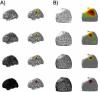
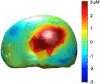
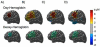
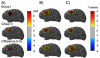
Diffuse optical imaging is a non-invasive technique for measuring changes in blood oxygenation in the brain. This technique is based on the temporally and spatially resolved recording of optical absorption in tissue within the near-infrared range of light. Optical imaging can be used to study functional brain activity similar to functional MRI. However, group level comparisons of brain activity from diffuse optical data are difficult due to registration of optical sensors between subjects. In addition, optical signals are sensitive to inter-subject differences in cranial anatomy and the specific arrangement of optical sensors relative to the underlying functional region. These factors can give rise to partial volume errors and loss of sensitivity and therefore must be accounted for in combining data from multiple subjects. In this work, we describe an image reconstruction approach using a parametric Bayesian model that simultaneously reconstructs group-level images of brain activity in the context of a random-effects analysis. Using this model, we demonstrate that localization accuracy and the statistical effects size of group-level reconstructions can be improved when compared to individualized reconstructions. In this model, we use the Restricted Maximum Likelihood (ReML) method to optimize a Bayesian random-effects model.
Keywords: (170.2655) Functional monitoring and imaging; (170.3010) Image reconstruction techniques.
Figures






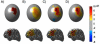


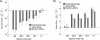

References
Grants and funding
LinkOut - more resources
Full Text Sources
