Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging
- PMID: 21337412
- PMCID: PMC3042509
- DOI: 10.1002/mrm.22655
Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging
Erratum in
- Magn Reson Med. 2011 May;65(5):1507
Abstract
This article presents two related advancements to the diffusional kurtosis imaging estimation framework to increase its robustness to noise, motion, and imaging artifacts. The first advancement substantially improves the estimation of diffusion and kurtosis tensors parameterizing the diffusional kurtosis imaging model. Rather than utilizing conventional unconstrained least squares methods, the tensor estimation problem is formulated as linearly constrained linear least squares, where the constraints ensure physically and/or biologically plausible tensor estimates. The exact solution to the constrained problem is found via convex quadratic programming methods or, alternatively, an approximate solution is determined through a fast heuristic algorithm. The computationally more demanding quadratic programming-based method is more flexible, allowing for an arbitrary number of diffusion weightings and different gradient sets for each diffusion weighting. The heuristic algorithm is suitable for real-time settings such as on clinical scanners, where run time is crucial. The advantage offered by the proposed constrained algorithms is demonstrated using in vivo human brain images. The proposed constrained methods allow for shorter scan times and/or higher spatial resolution for a given fidelity of the diffusional kurtosis imaging parametric maps. The second advancement increases the efficiency and accuracy of the estimation of mean and radial kurtoses by applying exact closed-form formulae.
Copyright © 2010 Wiley-Liss, Inc.
Figures
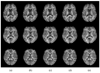



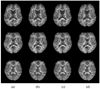
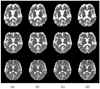

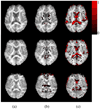
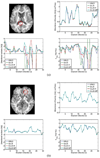
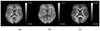
References
-
- Basser PJ. Inferring microstructural features and the physiological state of tissues from diffusion-weighted images. NMR in Biomedicine. 1995;8:333–344. - PubMed
-
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. Journal of Magnetic Resonance B. 1996;111:209–219. - PubMed
-
- Wedeen VJ, Hagmann P, Tseng W-YI, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magnetic Resonance in Medicine. 2005;54(6):1377–1386. - PubMed
-
- Jensen JH, Helpern JA. Quantifying non-Gaussian water diffusion by means of pulsed-field-gradient MRI; Toronto, Canada. Proceedings of the International Society for Magnetic Resonance in Medicine Annual Meeting; 2003. p. 2154.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

