A theoretical exploration of birhythmicity in the p53-Mdm2 network

Abstract

Experimental observations performed in the p53-Mdm2 network, one of the key protein modules involved in the control of proliferation of abnormal cells in mammals, revealed the existence of two frequencies of oscillations of p53 and Mdm2 in irradiated cells depending on the irradiation dose. These observations raised the question of the existence of birhythmicity, i.e. the coexistence of two oscillatory regimes for the same external conditions, in the p53-Mdm2 network which would be at the origin of these two distinct frequencies. A theoretical answer has been recently suggested by Ouattara, Abou-Jaoudé and Kaufman who proposed a 3-dimensional differential model showing birhythmicity to reproduce the two frequencies experimentally observed. The aim of this work is to analyze the mechanisms at the origin of the birhythmic behavior through a theoretical analysis of this differential model. To do so, we reduced this model, in a first step, into a 3-dimensional piecewise linear differential model where the Hill functions have been approximated by step functions, and, in a second step, into a 2-dimensional piecewise linear differential model by setting one autonomous variable as a constant in each domain of the phase space. We find that two features related to the phase space structure of the system are at the origin of the birhythmic behavior: the existence of two embedded cycles in the transition graph of the reduced models; the presence of a bypass in the orbit of the large amplitude oscillatory regime of low frequency. Based on this analysis, an experimental strategy is proposed to test the existence of birhythmicity in the p53-Mdm2 network. From a methodological point of view, this approach greatly facilitates the computational analysis of complex oscillatory behavior and could represent a valuable tool to explore mathematical models of biological rhythms showing sufficiently steep nonlinearities.

Figure 1. Experimental data from (Geva-Zatorsky et al., 2006, Fig.S3) .

Power spectrum of nuclear Mdm2-YFP fluorescence dynamics in individual cells. Top: an example of a cell showing fluctuations with a characteristic frequency of ∼10 hours (exposed to 0.3Gy of gamma irradiation), and the power spectrum of the signal (by Fourier transform). Bottom: an example of a cell with multiple oscillations with a period of ∼6 hours (exposed to 5Gy), and the power spectrum of the signal (right). Reprinted by permission from Macmillan Publishers Ltd: Molecular Systems Biology, advance online publication, 2006 (doi: 10.1038/msb4100068).

Figure 2. Schematic representation of the p53-Mdm2 core network.

Normal arrows correspond to positive interactions, blunt arrows to negative interactions. P, Mc and Mn represent p53, cytoplasmic Mdm2 and nuclear Mdm2 respectively.

Figure 3. Bifurcation diagram and projection of the phase portrait of birhythmicity in the plane (Mn,P) for Model 1.

(A) Bifurcation diagram of p53 level as a function of d_Mn for Model 1. Solid lines (resp. dashed lines) represent the stable (resp. unstable) equilibrium points. Bold (resp. white) dots are the maxima and minima of the stable (resp. unstable) limit cycles. The system shows a birhythmic domain for 1.75 h⁻¹<d_Mn<2.11 h⁻¹. (B) Projection of the two oscillatory regimes on the plane (Mn,P) for Model 1 for d_Mn = 1.9 h⁻¹. The thresholds K_Mc and K_Mn related to P are indicated in solid lines. The parameter values of Model 1 are the same as for the OAK Model (K_Mn = 0.1 nM) except: n = 6, d_P = 2.5 h⁻¹ and K_Mc = 0.4 nM (see legend of Figure S1 for the parameter values of the OAK Model).

Figure 4. Approximation of Hill function to step function.

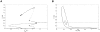
Hill function which appears in the equation of Mc in Model 1 (in black) and its approximation into the step function defined as: if and if (in red) for n = 6 and K_Mc = 0.4 nM. n is the Hill coefficient and characterizes the steepness of the Hill function.

Figure 5. Subdivision of the phase space and graph of transitions for Model 2.

(A) Subdivision of the phase space for Model 2 in 6 domains delimited by the thresholds K_P, K_Mn and K_Mc. (B) Graph of the transitions followed by the two oscillatory regimes composing birhythmicity shown in Figure 6. The small amplitude oscillatory regime of short period crosses domains D²², D¹², D¹³ and D²³ successively (in red). The large amplitude oscillatory regime of long period crosses domains: D²², D²¹, D¹¹, D¹², D¹³ and D²³ successively (in green).

Figure 6. Projection of the phase portrait of birhythmicity in the plane (Mn,P) for Model 2.

Projection of the two oscillatory regimes composing the birhythmic behavior of Model 2 in the plane (Mn,P). The dashed lines represent the thresholds of the step functions: K_Mn and K_Mc for P, K_P for Mn. The parameter values are the same as for Figure 3 (K_Mn = 0.1 nM, K_P = 0.2 nM) except K_Mc = 0.6 nM. The period of the large amplitude oscillatory regime is significantly longer than the period of the small amplitude oscillatory regime (see Figure 8A and 8C).

Figure 7. Subdivision of the phase space and transition graph for Model 3.

(A) Subdivision of the phase space for Model 3 in 8 domains delimited by the thresholds K_P, K_Mn, K_Mc and the additional threshold K (in red). (B) Transition graph of Model 3. The graph contains a branching point in domain D²³ and two embedded cycles. From this domain, the system can either go to domain D¹³ or domain D²² depending on the initial conditions.

Figure 8. Temporal simulations for Model 2 and Model 3.

Temporal simulation (h) of the concentration (in nM) of p53 (P), cytoplasmic Mdm2 (Mc) and nuclear Mdm2 (Mn) for Model 2 (A and C) and Model 3 (B and D) in the small amplitude short period (A and B) and the large amplitude long period (C and D) oscillatory regime. For Model 3, Mc has been set as a constant Mc^ij in each domain D^ij of the phase space following constraint (2) (see text). The parameter values are indicated in Figure 6 for Model 2 and in Figure 9 for Model 3.

Figure 9. Phase portrait of birhythmicity for Model 3.

Simulation of the two oscillatory regimes in the phase space for Model 3. The dashed lines represent the thresholds K_Mc, K_Mn and K for P, K_P for Mn. The parameter values are the same as for Figure 6 (K_Mn = 0.1 nM) except K_Mc = 0.4 nM, K = 0.05 nM, K_P = 2 nM, d_P = 3 h⁻¹, Mc¹¹ = Mc²¹ = Mc¹² = 0, Mc²² = 5 nM, Mc¹³ = 9 nM, Mc²³ = 11.3 nM, Mc¹⁴ =  Mc²⁴ = 25 nM. Note that, since the degradation constants d_Mn and d_P have the same values, the trajectories in each domain are straight lines.

Figure 10. First return map analysis for Model 3.

(A and C) In red, simulation in the phase plane for the initial conditions Mn = 2 nM and P = 0.515 nM (x>x_D, panel A) or P = 0.401 nM (x<x_D, panel C) for Model 3. The dashed lines represent the thresholds K_Mc = 0.4 nM, K_Mn = 0.1 nM and K = 0.05 nM for P, K_P = 2 nM for Mn. (B and D) In red, simulation of the orbit of the first return map from and to the [0, x) axis for the initials conditions of panel A (panel B) and panel C (panel D). The first return map F is shown in green and has been derived analytically (see Text S6). The parameter values are indicated in Figure 9. The discontinuity in F at x = x_D∼0.077 arises when the trajectory hits the threshold intersection point (Mn = K_P = 2, P = K_Mn = 0.1) (blue curve). The fixed points of F correspond to the two limit cycles of the system shown in Figure 9. For x>x_D (resp. x<x_D), the trajectory tends to the large (resp. small) amplitude oscillatory regime corresponding to the fixed point x = x₂∼0.093 (resp. x = x₁∼0.048).

Figure 11. Transition graph and first return map for the modified Model 3.

(A) Transition graph of the modified model 3. (B) Graph of the corresponding first return map (in green) from and to the [0, x) axis (see Figure 10). The parameter values are indicated in Figure 9, except Mc²² = 1. The focal point of D²² is now in D¹¹ inducing the additional transition from D²² to D¹² (arrow in red). The fixed points of the first return function correspond to limit cycles of the system. The system presents a unique limit cycle (x = x₁∼0.048) corresponding to the small amplitude oscillatory regime (see Figure 10C and 10D). The first return map shows a non smooth point at x_D∼0.077 (see Text S6).

Figure 12. Permanent shift from short to long period oscillatory regime after a transient p53 pulse.

Temporal simulation of p53 level for Model 3. A pulse of p53 is applied at t = 1.2 h (dashed line). Before applying the pulse, the system is oscillating in the small amplitude oscillatory regime. The p53 pulse induces a shift from the small amplitude short period to the large amplitude long period limit cycle. The parameter values are indicated in Figure 9.