Time and Associative Learning
- PMID: 21359131
- PMCID: PMC3045055
- DOI: 10.3819/ccbr.2010.50001
Time and Associative Learning
Abstract
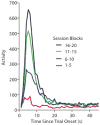
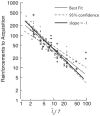
In a basic associative learning paradigm, learning is said to have occurred when the conditioned stimulus evokes an anticipatory response. This learning is widely believed to depend on the contiguous presentation of conditioned and unconditioned stimulus. However, what it means to be contiguous has not been rigorously defined. Here we examine the empirical bases for these beliefs and suggest an alternative view based on the hypothesis that learning about the temporal relationships between events determines the speed of emergence, vigor and form of conditioned behavior. This temporal learning occurs very rapidly and prior to the appearance of the anticipatory response. The temporal relations are learned even when no anticipatory response is evoked. The speed with which an anticipatory response emerges is proportional to the informativeness of the predictive cue (CS) regarding the rate of occurrence of the predicted event (US). This analysis gives an account of what we mean by "temporal pairing" and is in accord with the data on speed of acquisition and basic findings in the cue competition literature. In this account, learning depends on perceiving and encoding temporal regularities rather than stimulus contiguities.
Figures
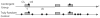






References
-
- Arcediano F, Escobar M, Miller RR. Temporal integration and temporal backward associations in human and nonhuman subjects. Learning & Behavior. 2003;31(3):242–256. - PubMed
-
- Arcediano F, Miller RR. Some constraints for models of timing: A temporal coding hypothesis perspective. Learning and Motivation. 2002;33(1):105–123.
-
- Babb SJ, Crystal JD. Discrimination of what, when, and where is not based on time of day. Learning & Behavior. 2006;34(2):124–130. - PubMed
-
- Balsam PD. The functions of context in learning and performance. In: Balsam P, Tomie A, editors. Context and Learning. Hillsdale, N.J: Lawrence Erlbaum Associates; 1985.
Grants and funding
LinkOut - more resources
Full Text Sources
