Reconstruction of brachytherapy seed positions and orientations from cone-beam CT x-ray projections via a novel iterative forward projection matching method

Abstract

Purpose: To generalize and experimentally validate a novel algorithm for reconstructing the 3D pose (position and orientation) of implanted brachytherapy seeds from a set of a few measured 2D cone-beam CT (CBCT) x-ray projections.

Methods: The iterative forward projection matching (IFPM) algorithm was generalized to reconstruct the 3D pose, as well as the centroid, of brachytherapy seeds from three to ten measured 2D projections. The gIFPM algorithm finds the set of seed poses that minimizes the sum-of-squared-difference of the pixel-by-pixel intensities between computed and measured autosegmented radiographic projections of the implant. Numerical simulations of clinically realistic brachytherapy seed configurations were performed to demonstrate the proof of principle. An in-house machined brachytherapy phantom, which supports precise specification of seed position and orientation at known values for simulated implant geometries, was used to experimentally validate this algorithm. The phantom was scanned on an ACUITY CBCT digital simulator over a full 660 sinogram projections. Three to ten x-ray images were selected from the full set of CBCT sinogram projections and postprocessed to create binary seed-only images.

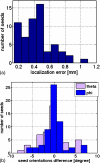
Results: In the numerical simulations, seed reconstruction position and orientation errors were approximately 0.6 mm and 5 degrees, respectively. The physical phantom measurements demonstrated an absolute positional accuracy of (0.78 +/- 0.57) mm or less. The theta and phi angle errors were found to be (5.7 +/- 4.9) degrees and (6.0 +/- 4.1) degrees, respectively, or less when using three projections; with six projections, results were slightly better. The mean registration error was better than 1 mm/6 degrees compared to the measured seed projections. Each test trial converged in 10-20 iterations with computation time of 12-18 min/iteration on a 1 GHz processor.

Conclusions: This work describes a novel, accurate, and completely automatic method for reconstructing seed orientations, as well as centroids, from a small number of radiographic projections, in support of intraoperative planning and adaptive replanning. Unlike standard back-projection methods, gIFPM avoids the need to match corresponding seed images on the projections. This algorithm also successfully reconstructs overlapping clustered and highly migrated seeds in the implant. The accuracy of better than 1 mm and 6 degrees demonstrates that gIFPM has the potential to support 2D Task Group 43 calculations in clinical practice.

Figure 1

Elongated line seed of length L is characterized by the seed center (black dot) positions (x,y,z) and orientation coordinates (θ,φ) angle pair in the world coordinates frame, where z is the axis of implantation.

Figure 2

Close-up photographs of (a) an acrylic slab of the phantom containing Model 6711 ¹²⁵I seeds, where the polar angle θ was defined as the angle between the implant axis and the major axis of the seed. It was assigned across the slab at different orientation for each seed (see inset). The azimuthal angle φ was assigned by using the adjustable reference grid drawn for each seed in known orientation. (b) Multiconfiguration precision-machined phantom assembly with all eight replaceable slabs. This phantom was used to create different seed configurations to test the gIFPM algorithm seed localization accuracy in the clinical setting.

Figure 3

An example case of the image postprocessing of the projection images obtained from the Varian 4030CB digital simulator, (a) raw projection image, (b) filtered image, (c) binary seed-only bitmap image, and (d) blurred grayscale image using the gIFPM algorithm for 76 seed phantom data sets.

Figure 4

An illustration of the convergence process for a 60 seed simulated implant. (a) Initial estimated seed configuration with straight seeds derived from a patient preplan, (b) computed images after convergence withσ₁=2.8 mm, (c) computed images after convergence with σ₂=1.8 mm and using poses (b) as the initial configuration, and (d) the true∕synthetic measured images, where the rows represent different gantry angles. The gIFPM algorithm was able to reproduce orientation of each individual seed including overlapping clustered and highly migrated seeds.

Figure 5

The similarity metric score vs iteration number for the two-step gIFPM algorithm for the four simulated patient cases: 56, 60, 66, and 70 seed configurations. The transition from larger to smaller blurring for the 66 seed configuration is shown by the black arrow. The one-dimensional image-intensity profiles in the inset illustrate the difference in capture range for the two blurring levels.

Figure 6

Histograms of the seed localization error for the 60 seed simulated patient configuration. (a) Positional error in terms of 3D distance between reconstructed and true location and (b) orientation error. The gIFPM absolute accuracy was (0.53±0.43) mm for position and (3.7±2.7)° and (4.5±3.8)° for θ and φ angles, respectively.

Figure 7

Illustration of gIFPM seed reconstruction for simulated case III in Table 1 for a single projection. In the first row(+20°), 66 seeds are present in the simulated implant derived from the preplan but 68 are assumed in the initial seed configure (a) with seed axes parallel to the gantry axis. In the second row(+20°), 66 seeds are present both in the initial estimated configuration and in the simulated implant, along with an additional seedlike artifact which is present in the measured images. (a) Initial estimate of the seed configuration, (b) computed images at final convergence, (c) the synthetic measured images corresponding to the “true” seed configuration, and (d) difference between images (b) and (c). The ellipse and arrow in part (d) indicates the extra seed(s) found by gIFPM at convergence.

Figure 8

The similarity metric score vs iteration number for the two-step gIFPM algorithm for the three example physical phantom seed configurations. The transition from larger to smaller blurring filter for the 50 seed configuration is highlighted by the black arrow.

Figure 9

Histograms of the seed localization error in 3D space between reconstructed and true pose for the 76 seed phantom configuration for three projection images. (a) Positional error and (b) orientation error. The RMS error was found to be (0.78±0.57) mm for position. The θ and φ angle distributions were found to be (5.7±4.9)° and(6.0±4.1)°, respectively.

Figure 10

Superposition of measured (white) and computed (black) line-seed images projected on the detector planes for gantry angles of (a) +5°, (b) −20°, and (c) +20°for 76 seed phantom configuration. While many computed seeds coincided exactly with the measured ones, a few still reveal small discrepancies.

Figure 11

Seed-by-seed vector difference between gIFPM positions and those obtained from the VARISEED planning system for 76 seed phantom data sets. The 3D RMS error was(1.69±0.63) mm.