Spin-orbit-coupled Bose-Einstein condensates
- PMID: 21368828
- PMCID: PMC11493149
- DOI: 10.1038/nature09887
Spin-orbit-coupled Bose-Einstein condensates
Abstract
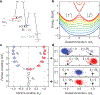
Spin-orbit (SO) coupling--the interaction between a quantum particle's spin and its momentum--is ubiquitous in physical systems. In condensed matter systems, SO coupling is crucial for the spin-Hall effect and topological insulators; it contributes to the electronic properties of materials such as GaAs, and is important for spintronic devices. Quantum many-body systems of ultracold atoms can be precisely controlled experimentally, and would therefore seem to provide an ideal platform on which to study SO coupling. Although an atom's intrinsic SO coupling affects its electronic structure, it does not lead to coupling between the spin and the centre-of-mass motion of the atom. Here, we engineer SO coupling (with equal Rashba and Dresselhaus strengths) in a neutral atomic Bose-Einstein condensate by dressing two atomic spin states with a pair of lasers. Such coupling has not been realized previously for ultracold atomic gases, or indeed any bosonic system. Furthermore, in the presence of the laser coupling, the interactions between the two dressed atomic spin states are modified, driving a quantum phase transition from a spatially spin-mixed state (lasers off) to a phase-separated state (above a critical laser intensity). We develop a many-body theory that provides quantitative agreement with the observed location of the transition. The engineered SO coupling--equally applicable for bosons and fermions--sets the stage for the realization of topological insulators in fermionic neutral atom systems.
Figures

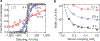

Comment in
-
Atomic physics: Atoms playing dress-up.Nature. 2011 Mar 3;471(7336):41-2. doi: 10.1038/471041a. Nature. 2011. PMID: 21368815 No abstract available.
References
-
- Kato YK, Myers RC, Gossard AC & Awschalom DD Observation of the spin Hall effect in semiconductors. Science 306, 1910–1913 (2004). - PubMed
-
- Konig M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007). - PubMed
-
- Kane CL & Mele EJ Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett 95,146802 (2005). - PubMed
-
- Bernevig BA, Hughes TL & Zhang S-C Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314,1757–1761 (2006). - PubMed
-
- Hsieh D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452,970–974 (2008). - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources

