An open source multivariate framework for n-tissue segmentation with evaluation on public data
- PMID: 21373993
- PMCID: PMC3297199
- DOI: 10.1007/s12021-011-9109-y
An open source multivariate framework for n-tissue segmentation with evaluation on public data
Abstract
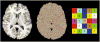
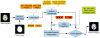
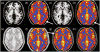
We introduce Atropos, an ITK-based multivariate n-class open source segmentation algorithm distributed with ANTs ( http://www.picsl.upenn.edu/ANTs). The Bayesian formulation of the segmentation problem is solved using the Expectation Maximization (EM) algorithm with the modeling of the class intensities based on either parametric or non-parametric finite mixtures. Atropos is capable of incorporating spatial prior probability maps (sparse), prior label maps and/or Markov Random Field (MRF) modeling. Atropos has also been efficiently implemented to handle large quantities of possible labelings (in the experimental section, we use up to 69 classes) with a minimal memory footprint. This work describes the technical and implementation aspects of Atropos and evaluates its performance on two different ground-truth datasets. First, we use the BrainWeb dataset from Montreal Neurological Institute to evaluate three-tissue segmentation performance via (1) K-means segmentation without use of template data; (2) MRF segmentation with initialization by prior probability maps derived from a group template; (3) Prior-based segmentation with use of spatial prior probability maps derived from a group template. We also evaluate Atropos performance by using spatial priors to drive a 69-class EM segmentation problem derived from the Hammers atlas from University College London. These evaluation studies, combined with illustrative examples that exercise Atropos options, demonstrate both performance and wide applicability of this new platform-independent open source segmentation tool.
Figures

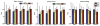



References
-
- Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26:839–851. - PubMed
-
- Aubert-Broche B, Griffin M, Pike GB, Evans AC, Collins DL. Twenty new digital brain phantoms for creation of validation image data bases. IEEE Transactions on Medical Imaging. 2006;25:1410–1416. - PubMed
-
- Avants B, Klein A, Tustison N, Woo J, Gee JC. Evaluation of open-access, automated brain extraction methods on multi-site multi-disorder data. 16th annual meeting for the Organization of Human Brain Mapping.2010b.
-
- Avants B, Cook PA, McMillan C, Grossman M, Tustison NJ, Zheng Y, et al. Sparse unbiased analysis of anatomical variance in longitudinal imaging. Proceedings of the 13th international conference on medical image computing and computer-assisted intervention (MICCAI); 2010c. pp. 324–331. - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

