Spike-based population coding and working memory
- PMID: 21379319
- PMCID: PMC3040643
- DOI: 10.1371/journal.pcbi.1001080
Spike-based population coding and working memory
Abstract
Compelling behavioral evidence suggests that humans can make optimal decisions despite the uncertainty inherent in perceptual or motor tasks. A key question in neuroscience is how populations of spiking neurons can implement such probabilistic computations. In this article, we develop a comprehensive framework for optimal, spike-based sensory integration and working memory in a dynamic environment. We propose that probability distributions are inferred spike-per-spike in recurrently connected networks of integrate-and-fire neurons. As a result, these networks can combine sensory cues optimally, track the state of a time-varying stimulus and memorize accumulated evidence over periods much longer than the time constant of single neurons. Importantly, we propose that population responses and persistent working memory states represent entire probability distributions and not only single stimulus values. These memories are reflected by sustained, asynchronous patterns of activity which make relevant information available to downstream neurons within their short time window of integration. Model neurons act as predictive encoders, only firing spikes which account for new information that has not yet been signaled. Thus, spike times signal deterministically a prediction error, contrary to rate codes in which spike times are considered to be random samples of an underlying firing rate. As a consequence of this coding scheme, a multitude of spike patterns can reliably encode the same information. This results in weakly correlated, Poisson-like spike trains that are sensitive to initial conditions but robust to even high levels of external neural noise. This spike train variability reproduces the one observed in cortical sensory spike trains, but cannot be equated to noise. On the contrary, it is a consequence of optimal spike-based inference. In contrast, we show that rate-based models perform poorly when implemented with stochastically spiking neurons.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

 during the read-out period. (B) Schematic illustration of the network. The visual and the auditory cue about stimulus
during the read-out period. (B) Schematic illustration of the network. The visual and the auditory cue about stimulus  are encoded in two independent input populations that send feed-forward inputs to the output population. The output population is recurrently connected. The connection weights
are encoded in two independent input populations that send feed-forward inputs to the output population. The output population is recurrently connected. The connection weights 
 and
and  are functions of the input kernels
are functions of the input kernels  and
and  as well as the output kernel
as well as the output kernel  . (C) Illustration of the spike generation rule.
. (C) Illustration of the spike generation rule.  denotes the stimulus posterior given all inputs and
denotes the stimulus posterior given all inputs and  represents an approximation to
represents an approximation to  that is decoded from the output spike trains.
that is decoded from the output spike trains.  should be as close as possible to
should be as close as possible to  . An output spike adds a kernel to
. An output spike adds a kernel to  . If its effect is to reduce the mean squared distance between the curves (down right), the spike is fired. The spike is not generated however if it increases the distance between the two curves (top right).
. If its effect is to reduce the mean squared distance between the curves (down right), the spike is fired. The spike is not generated however if it increases the distance between the two curves (top right).
 ) that codes for the stimulus diffusion. It has the effect of broadening the response during the memory period (see figure 3A).
) that codes for the stimulus diffusion. It has the effect of broadening the response during the memory period (see figure 3A).
 around its real value
around its real value  . The blue and red curves depict the performance of the ideal observer and the network respectively and the green curve shows the performance of a network without slow currents
. The blue and red curves depict the performance of the ideal observer and the network respectively and the green curve shows the performance of a network without slow currents  . (E) Width of the posterior decoded from the ideal observer (blue), the full network model (described in equations 7 and 8) (red), a network in which we approximate the nonlocal term in the slow currents
. (E) Width of the posterior decoded from the ideal observer (blue), the full network model (described in equations 7 and 8) (red), a network in which we approximate the nonlocal term in the slow currents  by a linear term (see equation 10) (green) and a network for which we completely remove the nonlocal term (magenta).
by a linear term (see equation 10) (green) and a network for which we completely remove the nonlocal term (magenta).
 . The effect is stronger for short integration times (200 ms, left) than for long integration times (500 ms, right). Black bars show the bias expected for a Bayesian observer, white bars depict the network bias. (C) Standard deviation of the estimator with a Gaussian prior (solid lines) and with a flat prior (dashed lines). A structured prior narrows the width of the posterior. Blue lines denote the ideal observer, red lines the network performance. (D) Input and output spike trains on a single trial. A constant stimulus is presented for 500 ms (gray area). The spontaneous activity before stimulus onset encodes the prior belief about the stimulus. (E) Time evolution of the posterior for the ideal observer (blue) and the network (red). Thick lines show the mean of the posterior and narrow lines the corresponding width. The stimulus is shown in black.
. The effect is stronger for short integration times (200 ms, left) than for long integration times (500 ms, right). Black bars show the bias expected for a Bayesian observer, white bars depict the network bias. (C) Standard deviation of the estimator with a Gaussian prior (solid lines) and with a flat prior (dashed lines). A structured prior narrows the width of the posterior. Blue lines denote the ideal observer, red lines the network performance. (D) Input and output spike trains on a single trial. A constant stimulus is presented for 500 ms (gray area). The spontaneous activity before stimulus onset encodes the prior belief about the stimulus. (E) Time evolution of the posterior for the ideal observer (blue) and the network (red). Thick lines show the mean of the posterior and narrow lines the corresponding width. The stimulus is shown in black.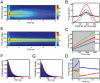
 for the regular parameters (red),
for the regular parameters (red),  (green) and
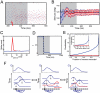
(green) and  (blue). (D) Traces of the average firing rate of three neurons whose preferred stimuli lie at the peak of the bump of activity (blue), the side of the bump (red) or far away from the bump (green). (E) PSTH of the output activity in response to a static stimulus presented for 500 ms. (F,G) Interspike interval (ISI) histogram during the integration period (F) and during the memory period (G) for a sample neuron. The red line shows the ISI histogram of a Poisson process with the same rate.
(blue). (D) Traces of the average firing rate of three neurons whose preferred stimuli lie at the peak of the bump of activity (blue), the side of the bump (red) or far away from the bump (green). (E) PSTH of the output activity in response to a static stimulus presented for 500 ms. (F,G) Interspike interval (ISI) histogram during the integration period (F) and during the memory period (G) for a sample neuron. The red line shows the ISI histogram of a Poisson process with the same rate.
 . Spikes are counted in 2 ms time bins and averaged over all neurons and over 10000 trials. (D) Time course of the normalized cross-correlation between the two runs of activity. The vertical dotted line indicates the time at which the perturbation (one extra spike) was added. (E) Predictability (equation 33) of the activity of an output neuron if we record from a fraction
. Spikes are counted in 2 ms time bins and averaged over all neurons and over 10000 trials. (D) Time course of the normalized cross-correlation between the two runs of activity. The vertical dotted line indicates the time at which the perturbation (one extra spike) was added. (E) Predictability (equation 33) of the activity of an output neuron if we record from a fraction  neurons of the output population. The predictability for neuron
neurons of the output population. The predictability for neuron  is plotted for spikes that are generated from the deterministic network (blue) or from a Poisson process (red). The rightmost predictability (at a fraction of 1) corresponds to the predictability of the measured, i.e. not predicted, membrane potential. The inset shows the increase in predictability previous to a spike (for a fraction of recorded neurons of 0.8). (F) Schematic illustration of the error correcting properties of the network. The left panel shows a reference spike train. Each spike adds a kernel that when added together give the log posterior G (top). If an extra spike is added (middle panel, red spike), the spike train is reshuffled in a way that keeps the total log posterior constant. If the initial spike fails to be elicited (right panel, blue dotted spike), a neighboring neuron recognizes the “hole” of information transmission and fires a spike to fill it. This changes the initial condition (first firing neuron in black) and therefore shuffles the spike train. The total log posterior remains the same.
is plotted for spikes that are generated from the deterministic network (blue) or from a Poisson process (red). The rightmost predictability (at a fraction of 1) corresponds to the predictability of the measured, i.e. not predicted, membrane potential. The inset shows the increase in predictability previous to a spike (for a fraction of recorded neurons of 0.8). (F) Schematic illustration of the error correcting properties of the network. The left panel shows a reference spike train. Each spike adds a kernel that when added together give the log posterior G (top). If an extra spike is added (middle panel, red spike), the spike train is reshuffled in a way that keeps the total log posterior constant. If the initial spike fails to be elicited (right panel, blue dotted spike), a neighboring neuron recognizes the “hole” of information transmission and fires a spike to fill it. This changes the initial condition (first firing neuron in black) and therefore shuffles the spike train. The total log posterior remains the same.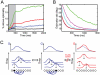
 (green),
(green),  (magenta) and
(magenta) and  (cyan). The ideal observer is plotted in blue and the performance of the deterministic network in red. A static stimulus is presented during the entire 1500 ms. (C) Schematic illustration of the difference between deterministic and stochastic spike generation. The left and middle panel show two spike trains encoding the same information but starting from different initial conditions. However, neurons in the output population are recurrently connected and “know” therefore perfectly well, when to fire a spike such that the log posterior
(cyan). The ideal observer is plotted in blue and the performance of the deterministic network in red. A static stimulus is presented during the entire 1500 ms. (C) Schematic illustration of the difference between deterministic and stochastic spike generation. The left and middle panel show two spike trains encoding the same information but starting from different initial conditions. However, neurons in the output population are recurrently connected and “know” therefore perfectly well, when to fire a spike such that the log posterior  is represented. If the lateral connections are removed, neurons fire stochastic spike trains that look similar to the deterministic ones but do not encode the same log posterior.
is represented. If the lateral connections are removed, neurons fire stochastic spike trains that look similar to the deterministic ones but do not encode the same log posterior.Similar articles
-
Including long-range dependence in integrate-and-fire models of the high interspike-interval variability of cortical neurons.Neural Comput. 2004 Oct;16(10):2125-95. doi: 10.1162/0899766041732413. Neural Comput. 2004. PMID: 15333210
-
Trial-to-Trial Variability of Spiking Delay Activity in Prefrontal Cortex Constrains Burst-Coding Models of Working Memory.J Neurosci. 2021 Oct 27;41(43):8928-8945. doi: 10.1523/JNEUROSCI.0167-21.2021. Epub 2021 Sep 22. J Neurosci. 2021. PMID: 34551937 Free PMC article.
-
Constructing Precisely Computing Networks with Biophysical Spiking Neurons.J Neurosci. 2015 Jul 15;35(28):10112-34. doi: 10.1523/JNEUROSCI.4951-14.2015. J Neurosci. 2015. PMID: 26180189 Free PMC article.
-
Nonrenewal spike train statistics: causes and functional consequences on neural coding.Exp Brain Res. 2011 May;210(3-4):353-71. doi: 10.1007/s00221-011-2553-y. Epub 2011 Jan 26. Exp Brain Res. 2011. PMID: 21267548 Free PMC article. Review.
-
Statistical models for neural encoding, decoding, and optimal stimulus design.Prog Brain Res. 2007;165:493-507. doi: 10.1016/S0079-6123(06)65031-0. Prog Brain Res. 2007. PMID: 17925266 Review.
Cited by
-
Efficient codes and balanced networks.Nat Neurosci. 2016 Mar;19(3):375-82. doi: 10.1038/nn.4243. Nat Neurosci. 2016. PMID: 26906504 Review.
-
Poisson balanced spiking networks.PLoS Comput Biol. 2020 Nov 20;16(11):e1008261. doi: 10.1371/journal.pcbi.1008261. eCollection 2020 Nov. PLoS Comput Biol. 2020. PMID: 33216741 Free PMC article.
-
On the number of neurons and time scale of integration underlying the formation of percepts in the brain.PLoS Comput Biol. 2015 Mar 20;11(3):e1004082. doi: 10.1371/journal.pcbi.1004082. eCollection 2015 Mar. PLoS Comput Biol. 2015. PMID: 25793393 Free PMC article.
-
Precise Spiking Motifs in Neurobiological and Neuromorphic Data.Brain Sci. 2022 Dec 29;13(1):68. doi: 10.3390/brainsci13010068. Brain Sci. 2022. PMID: 36672049 Free PMC article. Review.
-
Ensembles of spiking neurons with noise support optimal probabilistic inference in a dynamically changing environment.PLoS Comput Biol. 2014 Oct 23;10(10):e1003859. doi: 10.1371/journal.pcbi.1003859. eCollection 2014 Oct. PLoS Comput Biol. 2014. PMID: 25340749 Free PMC article.
References
-
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature. 2002;415:429–433. - PubMed
-
- Kording KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. - PubMed
-
- Knill DC, Richards W, editors. Perception as Bayesian inference. New York, NY, USA: Cambridge University Press; 1996.
-
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. - PubMed
-
- Zemel RS, Dayan P, Pouget A. Probabilistic interpretation of population codes. Neural Comput. 1998;10:403–430. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Research Materials

