Effect of promoter architecture on the cell-to-cell variability in gene expression
- PMID: 21390269
- PMCID: PMC3048382
- DOI: 10.1371/journal.pcbi.1001100
Effect of promoter architecture on the cell-to-cell variability in gene expression
Abstract
According to recent experimental evidence, promoter architecture, defined by the number, strength and regulatory role of the operators that control transcription, plays a major role in determining the level of cell-to-cell variability in gene expression. These quantitative experiments call for a corresponding modeling effort that addresses the question of how changes in promoter architecture affect variability in gene expression in a systematic rather than case-by-case fashion. In this article we make such a systematic investigation, based on a microscopic model of gene regulation that incorporates stochastic effects. In particular, we show how operator strength and operator multiplicity affect this variability. We examine different modes of transcription factor binding to complex promoters (cooperative, independent, simultaneous) and how each of these affects the level of variability in transcriptional output from cell-to-cell. We propose that direct comparison between in vivo single-cell experiments and theoretical predictions for the moments of the probability distribution of mRNA number per cell can be used to test kinetic models of gene regulation. The emphasis of the discussion is on prokaryotic gene regulation, but our analysis can be extended to eukaryotic cells as well.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
 and
and  , respectively and the rates of mRNA production for the basal and active states are
, respectively and the rates of mRNA production for the basal and active states are  and
and  respectively. The mRNA degradation rate is assumed to be constant for each molecule, and is given by the parameter
respectively. The mRNA degradation rate is assumed to be constant for each molecule, and is given by the parameter  . (B) List of all possible stochastic transitions affecting either the copy number of mRNA (m) or the state of the promoter (s) and their respective statistical weight. State 1 has the operator free. State 2 is the activator bound state. The weights represent the probability that each change of state will occur during a time increment
. (B) List of all possible stochastic transitions affecting either the copy number of mRNA (m) or the state of the promoter (s) and their respective statistical weight. State 1 has the operator free. State 2 is the activator bound state. The weights represent the probability that each change of state will occur during a time increment  . The master equation is constructed based on these rules.
. The master equation is constructed based on these rules.
 ), and transcription occurs at a constant rate r when the repressor falls off (with rate
), and transcription occurs at a constant rate r when the repressor falls off (with rate  ). (C) Normalized variance as a function of the fold-change in mean mRNA copy number. The parameters used are drawn from Table 1. The value of
). (C) Normalized variance as a function of the fold-change in mean mRNA copy number. The parameters used are drawn from Table 1. The value of  from Table 1 corresponds to the in vitro dissociation constant of the Lac repressor from the Oid operator (black). The results for an off-rate 10-times higher are also plotted (red). As a reference for the size of the fluctuations, we show the normalized variance for a Poisson promoter. (D) Fano factor for two promoters bearing the same off-rates as in (B). Inset. Prediction for the Fano factor for the ΔO3ΔO2PlacUV5 promoter, a variant of the PlacUV5 promoter for which the two auxiliary operators have been deleted. The fold-change in mRNA noise is plotted as a function of the fold-change in mean mRNA copy number for mutants of the promoter that replace O1 for Oid, O2 or O3. The parameters are taken from Table 1 and . Lifetimes of the operator-repressor complex are 7 min for Oid, 2.4 min for O1, 11s for O2 and 0.47 s for O3. (E) Fold-change in protein noise as a function of the fold-change in mean expression. As expected, the effect of operator strength is the same as observed for mRNA noise.
from Table 1 corresponds to the in vitro dissociation constant of the Lac repressor from the Oid operator (black). The results for an off-rate 10-times higher are also plotted (red). As a reference for the size of the fluctuations, we show the normalized variance for a Poisson promoter. (D) Fano factor for two promoters bearing the same off-rates as in (B). Inset. Prediction for the Fano factor for the ΔO3ΔO2PlacUV5 promoter, a variant of the PlacUV5 promoter for which the two auxiliary operators have been deleted. The fold-change in mRNA noise is plotted as a function of the fold-change in mean mRNA copy number for mutants of the promoter that replace O1 for Oid, O2 or O3. The parameters are taken from Table 1 and . Lifetimes of the operator-repressor complex are 7 min for Oid, 2.4 min for O1, 11s for O2 and 0.47 s for O3. (E) Fold-change in protein noise as a function of the fold-change in mean expression. As expected, the effect of operator strength is the same as observed for mRNA noise.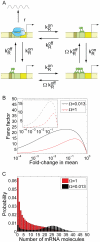
 and
and  are the rates of repressor dissociation and association to the operators, and
are the rates of repressor dissociation and association to the operators, and  is a parameter reflecting the effect of cooperative binding on the dissociation rate. For independent binding,
is a parameter reflecting the effect of cooperative binding on the dissociation rate. For independent binding,  and for cooperative binding
and for cooperative binding  (see Table 1). (B) Fold-change in the mRNA noise caused by gene regulation for independent (red) and cooperative (black) repression as a function of the mean mRNA copy number. Inset: Prediction for a variant of the λ PR promoter where the upstream operators OL1, OL2 and OL3 are deleted. The promoter mRNA noise is plotted as a function of the mean mRNA number for both wild-type cI repressor (blue line) and a repressor mutant (Y210H) that abolishes cooperativity (red line). Parameters taken from , . The lifetime of the OR1-cI complex is 4 min. Lifetime of OR2-cI complex is 9.5s. (C) mRNA distribution for the same parameters used in (B).
(see Table 1). (B) Fold-change in the mRNA noise caused by gene regulation for independent (red) and cooperative (black) repression as a function of the mean mRNA copy number. Inset: Prediction for a variant of the λ PR promoter where the upstream operators OL1, OL2 and OL3 are deleted. The promoter mRNA noise is plotted as a function of the mean mRNA number for both wild-type cI repressor (blue line) and a repressor mutant (Y210H) that abolishes cooperativity (red line). Parameters taken from , . The lifetime of the OR1-cI complex is 4 min. Lifetime of OR2-cI complex is 9.5s. (C) mRNA distribution for the same parameters used in (B).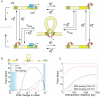
 and
and  are the rates of repressor dissociation and association. The rate of loop formation is
are the rates of repressor dissociation and association. The rate of loop formation is  , where
, where  can be thought of as the local concentration of repressor in the vicinity of one operator when it is bound to the other operator. The rate of dissociation of the operator-repressor complex in the looped conformation is given by
can be thought of as the local concentration of repressor in the vicinity of one operator when it is bound to the other operator. The rate of dissociation of the operator-repressor complex in the looped conformation is given by  . The parameter c captures the rate of repressor dissociation in the looped state relative to the rate of dissociation in a non-looped state. (B) Effect of DNA looping on cell-to-cell variability. The Fano factor is plotted as a function of the fold-change in the mean expression level, in the absence (blue) and presence (black) of the auxiliary operator, and assuming that dissociation of the operator from Om is the same in the looped and the unlooped state (c = 1). The presence of the auxiliary operator, which enables repression by DNA looping, increases the cell-to-cell variability. The regions over which the state with two repressors bound, the state with one repressor bound, or the looped DNA state are dominant are indicated by the shading in the background. The noise is larger at intermediate repression levels, where only one repressor is found bound to the promoter region, simultaneously occupying the auxiliary and main operators through DNA looping. The rate of DNA loop formation is
. The parameter c captures the rate of repressor dissociation in the looped state relative to the rate of dissociation in a non-looped state. (B) Effect of DNA looping on cell-to-cell variability. The Fano factor is plotted as a function of the fold-change in the mean expression level, in the absence (blue) and presence (black) of the auxiliary operator, and assuming that dissociation of the operator from Om is the same in the looped and the unlooped state (c = 1). The presence of the auxiliary operator, which enables repression by DNA looping, increases the cell-to-cell variability. The regions over which the state with two repressors bound, the state with one repressor bound, or the looped DNA state are dominant are indicated by the shading in the background. The noise is larger at intermediate repression levels, where only one repressor is found bound to the promoter region, simultaneously occupying the auxiliary and main operators through DNA looping. The rate of DNA loop formation is  . We also show the effect of DNA looping in the case where the kinetics of dissociation from the looped state are 100 times faster than the kinetics of dissociation from the unlooped state:
. We also show the effect of DNA looping in the case where the kinetics of dissociation from the looped state are 100 times faster than the kinetics of dissociation from the unlooped state:  (red). In this limit, the presence of the auxiliary operator leads to less gene expression noise. (C) Prediction for a library of PlacUV5 promoter variants, harboring an O2 deletion, and with the position of O3 moved upstream by multiples of 11 bp while keeping its identity (red), or replaced by the operator by Oid (black). Parameters are taken from the analysis in of the data in . We assume a concentration of 50 Lac repressor tetramers per cell. The association rate of the tetrameric repressor to the operators is taken from Table 1. The lifetimes of the operator-repressor complex are given in the caption to Figure 2. The dependence of the rate of DNA looping on the inter-operator distance is taken from , and equal to:
(red). In this limit, the presence of the auxiliary operator leads to less gene expression noise. (C) Prediction for a library of PlacUV5 promoter variants, harboring an O2 deletion, and with the position of O3 moved upstream by multiples of 11 bp while keeping its identity (red), or replaced by the operator by Oid (black). Parameters are taken from the analysis in of the data in . We assume a concentration of 50 Lac repressor tetramers per cell. The association rate of the tetrameric repressor to the operators is taken from Table 1. The lifetimes of the operator-repressor complex are given in the caption to Figure 2. The dependence of the rate of DNA looping on the inter-operator distance is taken from , and equal to:  , where
, where  ,
,  ,
,  ,
,  . Note that the Fano factor is not plotted as a function of the mean, but as a function of the inter-operator distance D. In this case, as we change D, we vary both the mean and the Fano factor.
. Note that the Fano factor is not plotted as a function of the mean, but as a function of the inter-operator distance D. In this case, as we change D, we vary both the mean and the Fano factor.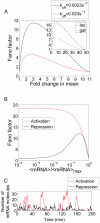
 , where f is the enhancement factor. Inset: Prediction for the activation of the Plac promoter. The fold-change in noise is plotted as a function of the fold-change in mean mRNA expression for both the wild-type Plac (CRP dissociation time = 8 min), represented by a blue line, and a Plac promoter variant where the lac CRP binding site has been replaced by the weaker gal CRP binding site (dissociation time = 1 min). The enhancement factor was set to
, where f is the enhancement factor. Inset: Prediction for the activation of the Plac promoter. The fold-change in noise is plotted as a function of the fold-change in mean mRNA expression for both the wild-type Plac (CRP dissociation time = 8 min), represented by a blue line, and a Plac promoter variant where the lac CRP binding site has been replaced by the weaker gal CRP binding site (dissociation time = 1 min). The enhancement factor was set to  . These parameters are taken from and . The remaining parameters are taken from Table 1. (B) Fano factor as a function of
. These parameters are taken from and . The remaining parameters are taken from Table 1. (B) Fano factor as a function of  for a repressor (black) and an activator (red) with the same transcription factor affinity. The transcription rate in the absence of activator is assumed to be zero. The transcription rate in the fully activated case is equal to the transcription rate of the repression construct in the absence of repressor and is
for a repressor (black) and an activator (red) with the same transcription factor affinity. The transcription rate in the absence of activator is assumed to be zero. The transcription rate in the fully activated case is equal to the transcription rate of the repression construct in the absence of repressor and is  as specified by Table 1. For low expression levels
as specified by Table 1. For low expression levels  simple activation is considerably noisier than simple repression. (C) The results of a stochastic simulation for the simple activation and simple repression architectures. We assume identical dissociation rates for the activator and repressor, and identical rates of transcription in their respective active states. As shown in (B), low concentrations of an activator result in few, but very productive transcription events, whereas high concentrations of a repressor lead to the frequent but short lived excursions into the active state.
simple activation is considerably noisier than simple repression. (C) The results of a stochastic simulation for the simple activation and simple repression architectures. We assume identical dissociation rates for the activator and repressor, and identical rates of transcription in their respective active states. As shown in (B), low concentrations of an activator result in few, but very productive transcription events, whereas high concentrations of a repressor lead to the frequent but short lived excursions into the active state.
 and
and  are the rates of activator dissociation and association to the operators, and
are the rates of activator dissociation and association to the operators, and  is a parameter reflecting the effect of cooperative binding on the dissociation rate. (B) Fano factor as a function of the mean mRNA for independent (
is a parameter reflecting the effect of cooperative binding on the dissociation rate. (B) Fano factor as a function of the mean mRNA for independent ( , black), cooperative (
, black), cooperative ( , red), and for simple activation (blue). The parameters are taken from Table 1 and
, red), and for simple activation (blue). The parameters are taken from Table 1 and  ,
,  ,
,  , and
, and  ; f is the enhancement factor. (C) A stochastic simulation shows the effect of independent and cooperative binding in creating a sustained state of high promoter activity, resulting in high levels of mRNA in the active state and large cell-to-cell variability. (D) Prediction for the r1-PRM promoter (a PRM promoter variant that does not exhibit OR3 mediated repression [51]). This promoter is activated by cI, which binds cooperatively to OR1 and OR2. The prediction is shown for wild-type cI (
; f is the enhancement factor. (C) A stochastic simulation shows the effect of independent and cooperative binding in creating a sustained state of high promoter activity, resulting in high levels of mRNA in the active state and large cell-to-cell variability. (D) Prediction for the r1-PRM promoter (a PRM promoter variant that does not exhibit OR3 mediated repression [51]). This promoter is activated by cI, which binds cooperatively to OR1 and OR2. The prediction is shown for wild-type cI ( ) and for a cooperativity deficient mutant (Y210H,
) and for a cooperativity deficient mutant (Y210H,  ). Parameters are taken from , , , . The lifetime of OR1-cI complex is 4 min. Lifetime of OR2-cI complex is 9.5 s.
). Parameters are taken from , , , . The lifetime of OR1-cI complex is 4 min. Lifetime of OR2-cI complex is 9.5 s.References
-
- Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. - PubMed
-
- Golding I, Paulsson J, Zawilski SM, Cox E. Real-time kinetics of gene activity in individual bacteria. Cell. 2005;123:1025–1036. - PubMed
-
- Cai L, Friedman N, Xie XS. Stochastic protein expression in individual cells at the single molecule level. Nature. 2006;440:358–362. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

