This site needs JavaScript to work properly. Please enable it to take advantage of the complete set of features!

Skip to main page content

Add to Collections

Your saved search

Name of saved search:

Search terms:

Test search terms

Would you like email updates of new search results?

Yes
No

Email: (change)

Frequency:

Which day?

Which day?

Report format:

Send at most:

Send even when there aren't any new results

Optional text in email:

Your RSS Feed

Review

. 2011 May;58(3-4):176-201.

doi: 10.1016/j.pnmrs.2010.10.003. Epub 2010 Dec 15.

Chemical shift tensors: theory and application to molecular structural problems

Julio C Facelli¹

Affiliations

Affiliation

¹ Department of Biomedical Informatics, Center for High Performance Computing, University of Utah, 155 South 1452 East RM 405, Salt Lake City, UT 84112-0190, USA. julio.facelli@utah.edu

PMID: 21397119
PMCID: PMC3058154
DOI: 10.1016/j.pnmrs.2010.10.003

Review

Chemical shift tensors: theory and application to molecular structural problems

Julio C Facelli. Prog Nucl Magn Reson Spectrosc. 2011 May.

. 2011 May;58(3-4):176-201.

doi: 10.1016/j.pnmrs.2010.10.003. Epub 2010 Dec 15.

Author

Julio C Facelli¹

Affiliation

¹ Department of Biomedical Informatics, Center for High Performance Computing, University of Utah, 155 South 1452 East RM 405, Salt Lake City, UT 84112-0190, USA. julio.facelli@utah.edu

PMID: 21397119
PMCID: PMC3058154
DOI: 10.1016/j.pnmrs.2010.10.003

No abstract available

PubMed Disclaimer

Figures

Fig. 1 — Fig. 1
Representative 25.1 MHz ¹³C NMR spectra of a single crystal of 1,3,5-trihydroxybenzene at different orientations with respect to the external magnetic field. From “Nuclear Magnetic Resonance Studies in Organic Single Crystals: Chemical Shift Anisotropy of Aromatic Molecules”, C.M. Carter, Ph.D. Thesis, The University of Utah, 1987.

Fig. 2 — Fig. 2
Powder pattern spectra for symmetric and asymmetric shielding tensors. From Ref. [23].

Fig. 3 — Fig. 3
Coordinate system used to illustrate the gauge origin dependence of the diamagnetic and paramagnetic contributions of the shielding. O is the origin of coordinates, O′ is the new origin of coordinates, R_O_′ is the position of the new origin of coordinates with respect to original one, R_N is the position of the nucleus N, r_k is the position of the electron with respect to O, r_Nk is the position of the electron with respect to the nucleus N and $r_{k}^{'}$ is the position of the electron relative to the new origin of coordinates O′.

Fig. 4 — Fig. 4
Basis set dependence of the ¹³CH₂ shieldings, δ, in glycine with different distributed gauge methods. SG: Single Gauge, IGAIM: Individual Gauge for Atoms in Molecules and GIAO: Gauge Including Atomic Orbitals. All the values are in ppm referenced to the bare nucleus. Calculations performed for the STO-3G, double zeta (DZ), triple zeta (TZ) and quadruple zeta (QZ) basis sets. From Ref. [135].

Fig. 5 — Fig. 5
Calculated ¹H shieldings (vertical axis) vs. experimental chemical shifts (horizontal axis) for different exchange-correlation functionals with the GIAO, CSGT and IGAIM approaches for selected molecules in the G2 and G3 set of molecules. From Ref. [191].

Fig. 6 — Fig. 6
Calculated ¹³C shieldings (vertical axis) vs. experimental chemical shifts (horizontal axis) for different exchange-correlation functionals with the GIAO, CSGT and IGAIM approaches for selected molecules in the G2 and G3 set of molecules. From Ref. [191].

Fig. 7 — Fig. 7
Calculated ¹⁵N shieldings (vertical axis) vs. experimental chemical shifts (horizontal axis) for different exchange-correlation functionals with the GIAO, CSGT and IGAIM approaches for selected molecules in the G2 and G3 set of molecules. From Ref. [191].

Fig. 8 — Fig. 8
Calculated ¹⁷O shieldings (vertical axis) vs. experimental chemical shifts (horizontal axis) for different exchange-correlation functionals with the GIAO, CSGT and IGAIM approaches for selected molecules in the G2 and G3 set of molecules. From Ref. [191].

Fig. 9 — Fig. 9
Linear correlation between calculated shielding and experimental shift tensor components. The lowest rmsd Hartree-Fock method, rhf/cc-pvdz, and DFT method, mwp1pw91/cc-pvtz, are plotted. The tensor parameters are in the icosahedral representation [194]. From Ref. [17].

Fig. 10 — Fig. 10
Haouamine A and the possible intermolecular motions that have been identified in this molecule (N-inversion and phenylene group rotation). Reproduced from Ref. [196].

Fig. 11 — Fig. 11
Fits between experimental and calculated ¹³C chemical shifts for menthol conformers with different dihedral angles of the isopropyl group. Reproduced from Ref. [197].

Fig. 12 — Fig. 12
Schematic structure of the naphthalene molecular tweezers host guest complex with dicyanobenzene guest. From Ref. [199].

Fig. 13 — Fig. 13
Unit cell of N,N-bis(diphenylphosphino)-N-((S)-α-methylbenzyl)amine and correlation between calculated and experimental ³¹P chemical shifts in the same compound. There are two resonances for each molecule for a total of eight different resonances. The points marked as stars correspond to the average chemical shifts for each molecule in the unit cell. From Ref. [215].

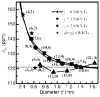
Fig. 14 — Fig. 14
Calculated ¹³C isotropic chemical shifts, δ_iso, of the zigzag (n ) 7–21 and four chiral (4, 2), (6, 2), (6, 3), and (8, 2) single-walled nanotubes (SWNTs) as a function of the tube diameter (d). The solid black lines are the fits to l = 1 and 2 zigzag SWNTs, respectively. Where l = mod(n − m, 3). The calculated δ_iso of an isolated graphene sheet is labeled as a black dashed line. The values of the semimetallic SWNTs are averaged over the maximal neighboring odd and even Monkhorst-Pack k-points. From Ref. [218].

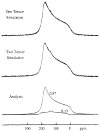
Fig. 15 — Fig. 15
Experimental and simulated (overlaid) static spectra of the Pennsylvania anthracene coal number PSOC-867. The lower trace shows the bands and relative intensities used to obtain the two tensor fit. Reproduced from Ref. [222].

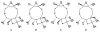
Fig. 16 — Fig. 16
Stereoisomers of artarborol that are consistent with the calculated ¹H and ¹³C chemical shifts. From Ref. [224].

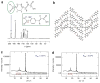
Fig. 17 — Fig. 17
(a) High-resolution solid state NMR spectrum for the β-polymorph of the p-formyl-trans-cinnamic acid with the proposed disorder of the formyl group shown in the insert. (b) Crystal structure of the β-polymorph of p-formyl-trans-cinnamic acid determined from powder X-ray diffraction data viewed along the a axis and with only the major orientation of the formyl group shown. Powder-ray diffraction Rietveld refinement of the β-polymorph of p-formyl-trans-cinnamic acid is shown in (c) and (d) for the ordered model of the formyl group (R_wp = 3.27%) and the disordered model of the formyl group (R_wp = 2.87%), respectively. Apart from the description of the order/disorder of the formyl group, all other aspects of the refinement calculations are the same for (c) and (d). The red boxes highlight the region of the powder X-ray diffraction pattern corresponding to the greatest improvement in the quality of the fit of the disordered model. From Ref. [226].

Fig. 18 — Fig. 18
Least-squares superposition of the chemical shift optimized structure with the original neutron diffraction structure of Nishiyama et al. [228] (shown as the transparent model). The rms difference for all atoms is 0.57 Å and 0.37 Å for heavy atoms alone. The unit cell is viewed from slightly below the origin of a/b/c. From Ref. [227].

Fig. 19 — Fig. 19
Calculated principal ¹³C chemical shift tensor components (δ₁₁, δ₂₂, δ₃₃) plotted against the experimental values. The values after optimization with isotropic chemical shift-pseudo forces are displayed as filled circles (●), while the result evaluated from the original (non-optimized) diffraction structure are open circles (○). From Ref. [227].

Fig. 20 — Fig. 20
The initial structure, solved using XRD for the heavy-atom positions and SSNMR for the OH hydrogen orientations, is in excellent agreement with diffraction data but gives a poor fit of the computed ¹³C shielding tensor principal values with the corresponding experimental data. This large error in the SSNMR fit indicated that further refinement was possible. A significant improvement in the fit (○) was obtained in the final refinement by adjusting bond lengths and valence angles computationally, while holding dihedral angles constant at XRD values. Computed shielding at sp² sites have systematic errors that are less problematic at sp³ carbons. The trend lines shown here are intended to show only overall improvement in the correlation and do not reflect these systematic differences. From Ref. [229].

Fig. 21 — Fig. 21
Atom numbering used in paclitaxel from Ref. [231].

Fig. 22 — Fig. 22
The five conformer models (a) providing high probability matches to the experimental chemical shift principal values of paclitaxel (form 2a) and the eight conformers (b) models providing probable matches to the experimental chemical shift principal values of paclitaxel (form 2b). From Ref. [231]

See this image and copyright information in PMC

References

1. Purcell EM. A precise determination of the proton magnetic moment in Bohr magnetons. Phys Rev. 76(1949):1262–1263.
1. Purcell EM, Torrey HC, Pound RV. Resonance absorption by nuclear magnetic moments in a solid. Phys Rev. 1946;69:37–38.
1. Ramsey NF. Magnetic shielding of nuclei in molecules. Phys Rev. 1950;78:699–703.
1. Ramsey NF. The internal diamagnetic field correction in measurements of the proton magnetic moment. Phys Rev. 1950;77:567.
1. Jameson CJ, de Dios AC. Theoretical and physical aspects of nuclear shielding, Nuclear Magnetic Resonance an Specialist Periodical Reports. The Royal Chemical Society; London: 2009. pp. 68–93.

Publication types

Actions
Actions
Actions

MeSH terms

Actions
Actions
Actions
Actions

Grants and funding

LinkOut - more resources

Full Text Sources