Analysis of molecular diffusion by first-passage time variance identifies the size of confinement zones

Abstract

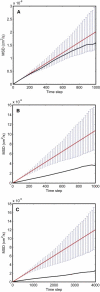
The diffusion of receptors within the two-dimensional environment of the plasma membrane is a complex process. Although certain components diffuse according to a random walk model (Brownian diffusion), an overwhelming body of work has found that membrane diffusion is nonideal (anomalous diffusion). One of the most powerful methods for studying membrane diffusion is single particle tracking (SPT), which records the trajectory of a label attached to a membrane component of interest. One of the outstanding problems in SPT is the analysis of data to identify the presence of heterogeneity. We have adapted a first-passage time (FPT) algorithm, originally developed for the interpretation of animal movement, for the analysis of SPT data. We discuss the general application of the FPT analysis to molecular diffusion, and use simulations to test the method against data containing known regions of confinement. We conclude that FPT can be used to identify the presence and size of confinement within trajectories of the receptor LFA-1, and these results are consistent with previous reports on the size of LFA-1 clusters. The analysis of trajectory data for cell surface receptors by FPT provides a robust method to determine the presence and size of confined regions of diffusion.

Figure 1

Experimental trajectories of LFA-1 fail the CRW model. Mean-squared displacement (MSD) was calculated for simulated and experimental trajectories (solid dark line), and compared to the expected MSD curve (solid light line). Pseudotrajectories were calculated from the trajectory data to provide the pseudotrajectory envelope (bars). MSD curves that fall outside the envelope are considered to have failed the CRW model (see Methods). (A) Testing the CRW model for a population of simulated trajectories with a uniform turning angle distribution and normal length distribution. The length distribution was based on D = 5 × 10⁻¹² cm² s⁻¹ (number of pseudotrajectories per group, n = 50; number of pseudotrajectory groups, m = 500). (B) Rejecting the CRW model for a population of simulated trajectories with the added characteristic of moving in and out of confinement zones (n = 50, m = 500). The probabilities of entering or leaving a confinement zone are given by p_i = 0.9 and p_o = 0.1, respectively. (C) Rejecting the CRW model for experimental LFA-1 trajectories (TS1/18 labeled LFA-1, DMSO-treated cells; n = 75, m= 500).

Figure 2

First-passage time analysis of simulated trajectories. Each curve depicts the variance of FPT, S(r), averaged over a population of 20 trajectories. (A) Trajectories were simulated with D = 5 × 10⁻¹² cm² s⁻¹ and confinement zones with radius r_c = 50 nm (red), 100 nm (green), 200 nm (blue), 500 nm (magenta), and 1000 nm (black), and probabilities p_i = 1 and p_o = 0. (B) Trajectories were simulated with D = 5 × 10⁻¹² cm² s⁻¹ and a transient confinement model with probability p_i = 0.05 (red), 0.2 (green), 0.4 (blue), 0.8 (magenta), and 0.9 (black), p_o = 0.1, and r_c = 50 nm. (C) Trajectories were simulated with D = 5 × 10⁻¹² cm² s⁻¹ and a transient confinement model with p_o = 0.05 (red), 0.2 (green), 0.4 (blue), 0.8 (magenta), and 1 (black), p_i = 0.1, and r_c = 50 nm. (D) Representative simulated trajectories are shown and are labeled using the same colors and a lowercase letter as above. Scale bar = 1 μm.

Figure 3

First-passage time analysis of TS1/18-labeled LFA-1 on resting cells. Experimental trajectories of TS1/18-labeled LFA-1 collected on untreated cells (n = 75) were classified based on the occurrence and range of a peak in S(r), or whether they were not rejected for CRW. For clarity, trajectories are plotted with peaks occurring within (A) 0–50 nm, (B) 50–150 nm, and (C) >150 nm. (D) Trajectories that were not rejected for CRW. Individual FPT curves are plotted in gray, and the average curve for each category is plotted in black. (E) Collected average S(r) curves from (A–D) are shown overlaid and are labeled with a corresponding lowercase letter. (F) Sample trajectories from the populations sorted into (A–D) are shown and labeled by a corresponding lowercase letter. Scale bar = 1 μm.

Figure 4

Population analysis of LFA-1 trajectories based on FPT. (A) The average S(r) for all TS1/18-labeled LFA-1 trajectories, with significant peak height (>0.5) and for which the CRW model was rejected, in the control (solid line) and PMA-treated (dashed line) data sets. Both data sets had a large proportion of trajectories for which the CRW model was rejected, and both show apparent FPT peaks when the average S(r) curve is calculated. (B) The average S(r) for all MEM148-labeled LFA-1 trajectories, with significant peak height (>0.5) and for which the CRW model was rejected, in the control (solid line) and PMA-treated (dashed line) data sets. Curves for simulated free diffusion are also shown (filled gray) for comparison. Distributions of peak locations detected by FPT analysis and CRW testing are shown for (C) LFA-1 trajectories on Jurkat cells (MEM148 labeled, DMSO control) and (D) LFA-1 trajectories on activated Jurkat cells (MEM148 labeled, PMA-treated). Curves represent a population density analysis of the same data shown in the histogram plot (67).