A competitive network theory of species diversity
- PMID: 21415368
- PMCID: PMC3078357
- DOI: 10.1073/pnas.1014428108
A competitive network theory of species diversity
Abstract
Nonhierarchical competition between species has been proposed as a potential mechanism for biodiversity maintenance, but theoretical and empirical research has thus far concentrated on systems composed of relatively few species. Here we develop a theory of biodiversity based on a network representation of competition for systems with large numbers of competitors. All species pairs are connected by an arrow from the inferior to the superior. Using game theory, we show how the equilibrium density of all species can be derived from the structure of the network. We show that when species are limited by multiple factors, the coexistence of a large number of species is the most probable outcome and that habitat heterogeneity interacts with network structure to favor diversity.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

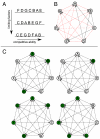

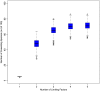
Comment in
-
Weak points in competitive network theory of species diversity.Proc Natl Acad Sci U S A. 2011 Aug 2;108(31):E345; author reply E346. doi: 10.1073/pnas.1108391108. Epub 2011 Jul 8. Proc Natl Acad Sci U S A. 2011. PMID: 21742985 Free PMC article. No abstract available.
References
-
- Hutchinson GE. The paradox of the plankton. Am Nat. 1961;95:137–141.
-
- Gause GF. The Struggle for Existence. New York: Hafner Press; 1934. - PubMed
-
- Hubbell SP. The Unified Neutral Theory of Biodiversity and Biogeography. Princeton, NJ: Princeton Univ Press; 2001. - PubMed
-
- Chave J. Neutral theory and community ecology. Ecol Lett. 2004;7:241–253.
-
- Alonso D, Etienne R, McKane A. The merits of neutral theory. Trends Ecol Evol. 2006;21:451–457. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

