To lyse or not to lyse: transient-mediated stochastic fate determination in cells infected by bacteriophages

Abstract

Cell fate determination is usually described as the result of the stochastic dynamics of gene regulatory networks (GRNs) reaching one of multiple steady-states each of which corresponds to a specific decision. However, the fate of a cell is determined in finite time suggesting the importance of transient dynamics in cellular decision making. Here we consider cellular decision making as resulting from first passage processes of regulatory proteins and examine the effect of transient dynamics within the initial lysis-lysogeny switch of phage λ. Importantly, the fate of an infected cell depends, in part, on the number of coinfecting phages. Using a quantitative model of the phage λ GRN, we find that changes in the likelihood of lysis and lysogeny can be driven by changes in phage co-infection number regardless of whether or not there exists steady-state bistability within the GRN. Furthermore, two GRNs which yield qualitatively distinct steady state behaviors as a function of phage infection number can show similar transient responses, sufficient for alternative cell fate determination. We compare our model results to a recent experimental study of cell fate determination in single cell assays of multiply infected bacteria. Whereas the experimental study proposed a "quasi-independent" hypothesis for cell fate determination consistent with an observed data collapse, we demonstrate that observed cell fate results are compatible with an alternative form of data collapse consistent with a partial gene dosage compensation mechanism. We show that including partial gene dosage compensation at the mRNA level in our stochastic model of fate determination leads to the same data collapse observed in the single cell study. Our findings elucidate the importance of transient gene regulatory dynamics in fate determination, and present a novel alternative hypothesis to explain single-cell level heterogeneity within the phage λ lysis-lysogeny decision switch.

Figure 1. Core genetic components of lysis-lysogeny decision switch in phage .

(A) Schematic diagram of genes and promoters. CI and CRO dimers are the transcription factors for and while and is controlled by CII tetramers. Black arrows represent open reading frames of promoters when activated (, and ) and antisense transcript aQ. (B) Interactions among gene products. Regular and blunt arrows represent positive and negative feedbacks, respectively. CI dimers are self-activators while repressing the other genes, and CRO dimers repress all the genes in the system. CII tetramers activate cI transcription, and suppress Q expression by transcribing antisense mRNAs.

Figure 2. Dynamics of regulatory proteins, CI and Q, when the GRN is asymptotically divergent and transiently divergent.

(A) Phase diagram of CI-Q dynamics when asymptotically divergent for . Note that the system is bistable. (B) Phase diagram of CI-Q dynamics starting from no viral proteins when asymptotically divergent. Thresholds of CI and Q (both at 100 nM) represent the concentrations above which decisions are lysogenic and lytic, respectively. Trajectories cross the threshold only once. (C) Asymptotically divergent dynamics of Q concentration as a function of time. (D) Phase diagram of transiently divergent system with . Note that the system is not bistable. (E) Phase diagram of CI-Q dynamics of the transiently divergent phage GRN. At the deterministic trajectory crosses the threshold three times, and decisions change from lysis to lysogeny as a function of time. (F) Transiently divergent Q dynamics.

Figure 3. Stochastic realization of C and Q dynamics for (A) and (B) .

Trajectories are sampled for every 1/4 minute. The system is transiently divergent, and thresholds are set at 100 nM for both CI and Q. Each curve represents a single realization, and 50 realizations are shown here. Red trajectories indicate that decisions are lytic whereas blue ones represent lysogeny.

Figure 4. Response of phage to various phage genome concentrations when (A) asymptotically divergent and (B) transiently divergent.

and represent the number of coinfecting phages and the host cell volume, respectively, so is the phage genome concentration. Each point is the result from 5,000 simulations.

Figure 5. Alternative mechanisms underlying heterogeneity of lysis-lysogeny decisions.

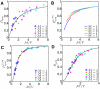
(A) Fraction of lysogeny plotted from single cell assays. (B) Rescaled probability of . Each phage within a host is completely independent from other phages, and decision of lysogeny becomes a function of host volume. Note that rescaled curves do not collapse into a single curve. (C) Rescaled probability of proposed by Zeng et. al. representing the probability of lysogeny for each individual infecting phage. Each phage independently “chooses” lysis or lysogeny. However, since the fraction of lysogeny for a single phage is a function of , phages sense the presence of other phages. Note that data from different -s collapse into a single curve. (D) Probability of lysogeny plotted against rescaled when , corresponding to a mechanism in which gene expression from multiple copies is partially compensated. Due to partial dosage compensation, the transcription rate is not linearly proportional to , and the effective copy number is given as where . Note that the data from different -s collapse into a single curve. Black lines represent nonlinear curve fits into Hill functions.

Figure 6. Effect of gene dosage compensation from stochastic simulations.

(A) Fraction of lysogeny from stochastic simulations. Simulations with partial dosage compensation exhibit the nested pattern of dependence as seen in the experimental data (see Fig. 5). (B) Simulation results on the fraction of lysogeny from Fig. 6 (A) plotted with rescaled when . The outcome of stochastic simulations with partial dosage compensation is consistent with experimental data (see Fig. 5 (A,D)). In this case, the GRN is asymptotically driven with CI and Q threshold at 100 nM and 120 nM, respectively, all other parameters are set according to Table 1 - transiently divergent. Each point is the result from 3,000 simulations.