Material property estimation for tubes and arteries using ultrasound radiation force and analysis of propagating modes

Abstract

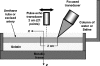
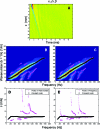
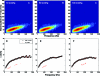
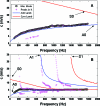
Arterial elasticity has been proposed as an independent predictor of cardiovascular diseases and mortality. Identification of the different propagating modes in thin shells can be used to characterize the elastic properties. Ultrasound radiation force was used to generate local mechanical waves in the wall of a urethane tube or an excised pig carotid artery. The waves were tracked using pulse-echo ultrasound. A modal analysis using two-dimensional discrete fast Fourier transform was performed on the time-space signal. This allowed the visualization of different modes of propagation and characterization of dispersion curves for both structures. The urethane tube/artery was mounted in a metallic frame, embedded in tissue-mimicking gelatin, cannulated, and pressurized over a range of 10-100 mmHg. The k-space and the dispersion curves of the urethane tube showed one mode of propagation, with no effect of transmural pressure. Fitting of a Lamb wave model estimated Young's modulus in the urethane tube around 560 kPa. Young's modulus of the artery ranged from 72 to 134 kPa at 10 and 100 mmHg, respectively. The changes observed in the artery dispersion curves suggest that this methodology of exciting mechanical waves and characterizing the modes of propagation has potential for studying arterial elasticity.

Figure 1

Color online A tube submerged in water is approximated by an elastic homogenous plate submerged in an incompressible fluid. The motion shown is an antisymmetric mode.

Figure 2

Color online Experimental setup for urethane or excised pig artery. A focused ultrasound transducer was used to generate mechanical waves and pulse-echo transducer was used to measure the speed of the propagating wave. A column of water was used to change the transmural pressure. Both the tube and the artery were embedded in a gelatin which mimics the surrounding properties of tissue.

Figure 3

Diagram describing the process to determine the dispersion curves for the tube and the artery from the time–space signal. Panel A shows an example of a guided wave propagating in time and space in an arterial wall. Panels B and C shows the masked 2D DFFT or H(k, f) of the signal in panel A, where the x-axis represents frequency and the y-axis the wave number (k = 1∕λ, where λ is the wavelength). Black circles show the dominant or highest energy mode for each frequency [first antisymmetric Lamb wave-like mode (A0)]. In panel B, the magenta crosses represent the peaks found using the partial derivative in the frequency direction, corresponding to higher order modes. Similarly in panel C, the magenta crosses represent the peaks found using the partial derivative in the wave number direction. Panels D and E show the dispersion curves; as in panels B and C, the black circles show the mode of maximum energy and the magenta crosses the higher order modes.

Figure 4

Panel A shows the time-space propagation of a guided wave over 20 mm. Panel B shows three representative time signals at 5, 10, and 20 mm from the excitation point. Panel C shows the respective frequency spectra [H(f)] of the time signals presented in panel B.

Figure 5

K-space and dispersion diagrams for urethane tube. Panels A, B, and C show the k-space representation for the urethane tube at three different pressures (10, 50, and 100 mmHg). Panels D, E, and F show the respective dispersion diagrams, where the black circles represent the highest energy mode and the red crosses the peaks found in the frequency direction. The peak results in the wave number direction are not presented since they only added noise to the figures.

Figure 6

K-space and dispersion diagrams for excised pig carotid artery. Panels A, B, and C show the k-space representation for the artery at three different pressures (10, 50, and 100 mmHg). Panels D, E, and F show the respective dispersion diagrams, where the black circles represent the highest energy mode and the red crosses the peaks in the wave number direction. The peak results in the frequency direction are not presented since they failed to track the higher order modes.

Figure 7

Experimental dispersion curves and fitting of a Lamb wave model. Panel A shows the dispersion curve for the urethane tube at 50 mmHg. The black circles represent the highest energy mode while the magenta circles the peaks in the wave number direction. The blue and the red lines represent the antisymmetric (A) and symmetric (S) modes for the Lamb wave model. Similarly, panel B show the dispersion curves and Lamb wave fitting for the artery at 50 mmHg. The legend from panel A applies to panel B.