Modeling subharmonic response from contrast microbubbles as a function of ambient static pressure

Abstract

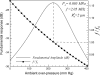
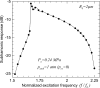
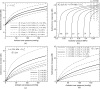
Variation of subharmonic response from contrast microbubbles with ambient pressure is numerically investigated for non-invasive monitoring of organ-level blood pressure. Previously, several contrast microbubbles both in vitro and in vivo registered approximately linear (5-15 dB) subharmonic response reduction with 188 mm Hg change in ambient pressure. In contrast, simulated subharmonic response from a single microbubble is seen here to either increase or decrease with ambient pressure. This is shown using the code BUBBLESIM for encapsulated microbubbles, and then the underlying dynamics is investigated using a free bubble model. The ratio of the excitation frequency to the natural frequency of the bubble is the determining parameter--increasing ambient pressure increases natural frequency thereby changing this ratio. For frequency ratio below a lower critical value, increasing ambient pressure monotonically decreases subharmonic response. Above an upper critical value of the same ratio, increasing ambient pressure increases subharmonic response; in between, the subharmonic variation is non-monotonic. The precise values of frequency ratio for these three different trends depend on bubble radius and excitation amplitude. The modeled increase or decrease of subharmonic with ambient pressure, when one happens, is approximately linear only for certain range of excitation levels. Possible reasons for discrepancies between model and previous experiments are discussed.

Figure 1

(a) Fractional change in initial radius of a free bubble due to change in ambient pressure and (b) fractional change in linear resonance frequency due to change in ambient pressure.

Figure 2

Change in the subharmonic response of mono-dispersed contrast microbubbles with a 32-cycle rectangular driving pulse for (a) Levovist (R₀ = 3 μm and P_A = 0.8 MPa) and (b) Sonazoid (R₀ = 3.2 μm and P_A = 0.4 MPa) as per BUBBLESIM.

Figure 3

Variation of fundamental response of a 2 μm free microbubble with ambient over-pressure and normalized excitation frequency f ∕ f₀.

Figure 4

Variation of the subharmonic response of a 2 μm radius free bubble with normalized excitation frequency f ∕ f₀.

Figure 5

Variation of subharmonic response (a) with ambient over-pressure for free bubbles of radius $R_0^0=0\mathrm{.}5\mathrm{,}1\mathrm{,}1\mathrm{.}5\mathrm{,}2\mathrm{,}2\mathrm{.}5\mathrm{,}3\mathrm{,}4$, and $5\mu \mathrm{m}$ at respective excitation frequencies such that $f=1.5f_0^0$, (b) with excitation pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at $f=2.627\mathrm{MHz}=1.5f_0^0$, (c) with ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at fixed excitation frequency $(f=2.627\mathrm{MHz}=1.5f_0^0)$ and different excitation pressures, and (d) with the ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies.

Figure 6

Variation of subharmonic response (a) with excitation pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies and zero ambient over-pressure, (b) with ambient over-pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies and P_A = 0.3 MPa, and (c) with ambient over-pressure for free bubbles of radius $R_0^0=1,2,3,4$, and $5\mu \mathrm{m}$ at excitation frequencies such that $f=1.8f_0^0$.

Figure 7

Variation of subharmonic response (a) with ambient over-pressure for free bubbles of radius $R_0^0=0\mathrm{.}5\mathrm{,}1\mathrm{,}1\mathrm{.}5\mathrm{,}2\mathrm{,}2\mathrm{.}5\mathrm{,}3\mathrm{,}4$, and $5\mu \mathrm{m}$ at excitation frequencies such that $f=2.5f_0^0$, (b) with excitation pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at $f=4.3784\mathrm{MHz}\mathrm{=}2.5f_0^0$, (c) with ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at fixed excitation frequency $(f=4.3784\mathrm{MHz}\mathrm{=}2.5f_0^0)$ and different excitation pressures, and (d) with ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies.