Effects of intima stiffness and plaque morphology on peak cap stress

Abstract

Background: Rupture of the cap of a vulnerable plaque present in a coronary vessel may cause myocardial infarction and death. Cap rupture occurs when the peak cap stress exceeds the cap strength. The mechanical stress within a cap depends on the plaque morphology and the material characteristics of the plaque components. A parametric study was conducted to assess the effect of intima stiffness and plaque morphology on peak cap stress.

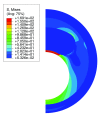
Methods: Models with idealized geometries based on histology images of human coronary arteries were generated by varying geometric plaque features. The constructed multi-layer models contained adventitia, media, intima, and necrotic core sections. For adventitia and media layers, anisotropic hyperelastic material models were used. For necrotic core and intima sections, isotropic hyperelastic material models were employed. Three different intima stiffness values were used to cover the wide range reported in literature. According to the intima stiffness, the models were classified as stiff, intermediate and soft intima models. Finite element method was used to compute peak cap stress.

Results: The intima stiffness was an essential determinant of cap stresses. The computed peak cap stresses for the soft intima models were much lower than for stiff and intermediate intima models. Intima stiffness also affected the influence of morphological parameters on cap stresses. For the stiff and intermediate intima models, the cap thickness and necrotic core thickness were the most important determinants of cap stresses. The peak cap stress increased three-fold when the cap thickness was reduced from 0.25 mm to 0.05 mm for both stiff and intermediate intima models. Doubling the thickness of the necrotic core elevated the peak cap stress by 60% for the stiff intima models and by 90% for the intermediate intima models. Two-fold increase in the intima thickness behind the necrotic core reduced the peak cap stress by approximately 25% for both intima models. For the soft intima models, cap thickness was less critical and changed the peak cap stress by 55%. However, the necrotic core thickness was more influential and changed the peak cap stress by 100%. The necrotic core angle emerged as a critical determinant of cap stresses where a larger angle lowered the cap stresses. Contrary to the stiff and intermediate intima models, a thicker intima behind the necrotic core increased the peak cap stress by approximately 25% for the soft intima models. Adventitia thickness and local media regression had limited effects for all three intima models.

Conclusions: For the stiff and intermediate intima models, the cap thickness was the most important morphological risk factor. However for soft intima models, the necrotic core thickness and necrotic core angle had a bigger impact on the peak cap stress. We therefore need to enhance our knowledge of intima material properties if we want to derive critical morphological plaque features for risk evaluation.

Figure 1

Examples of coronary artery plaques having different geometric features: histological cross-sections (upper panel), and corresponding color-coded, manually drawn contours (lower panel). Key to the colors used: brown = adventitia, red = media, yellow = intima, and orange = necrotic core. White arrows indicate the locations with a thick intima layer and black arrows indicate the locations with a thin intima layer behind the necrotic core. Stars show severely compromised media.

Figure 2

Examples of computational models. The model on the left panel shows different geometric features: α= Necrotic core angle, a= Adventitia thickness, b= Media thickness, c= Intima thickness behind the necrotic core, d= Necrotic core thickness, and e= Cap thickness. The model on the right panel shows local media regression in the center. S indicates shoulder region and M indicates midcap region. Key to the colors used: brown=adventitia, red=media, yellow= intima, and orange=necrotic core.

Figure 3

Contour map of von Mises stresses in half cross-section of a plaque model with intermediate intima stiffness. The highest stresses are in the cap and the peak stress values in the midcap and shoulder region are similar.

Figure 4

Influence of the cap thickness and intima stiffness on the peak cap stress for the baseline geometry. Constant parameter values for the models: necrotic core thickness = 1.2 mm, intima thickness behind the necrotic core = 0.5 mm, adventitia thickness = 0.15 mm, media thickness = 0.25 mm, necrotic core angle = 30°. Peak cap stress values and the undeformed geometries of some models are attached to the associated columns. The Young's modulus (E) values for the intima: 33 kPa for soft, 500 kPa for intermediate and 1000 kPa for stiff.

Figure 5

Influence of the necrotic core thickness and intima stiffness on the peak cap stress for the baseline geometry. Constant parameter values for the models: cap thickness = 0.05 mm, intima thickness behind the necrotic core = 0.5 mm, adventitia thickness = 0.15 mm, media thickness = 0.25 mm, necrotic core angle = 30°. Peak cap stress values and the undeformed geometries of some models are attached to the associated columns. The Young's modulus (E) values for the intima: 33 kPa for soft, 500 kPa for intermediate and 1000 kPa for stiff.