How simple rules determine pedestrian behavior and crowd disasters
- PMID: 21502518
- PMCID: PMC3084058
- DOI: 10.1073/pnas.1016507108
How simple rules determine pedestrian behavior and crowd disasters
Abstract
With the increasing size and frequency of mass events, the study of crowd disasters and the simulation of pedestrian flows have become important research areas. However, even successful modeling approaches such as those inspired by Newtonian force models are still not fully consistent with empirical observations and are sometimes hard to calibrate. Here, a cognitive science approach is proposed, which is based on behavioral heuristics. We suggest that, guided by visual information, namely the distance of obstructions in candidate lines of sight, pedestrians apply two simple cognitive procedures to adapt their walking speeds and directions. Although simpler than previous approaches, this model predicts individual trajectories and collective patterns of motion in good quantitative agreement with a large variety of empirical and experimental data. This model predicts the emergence of self-organization phenomena, such as the spontaneous formation of unidirectional lanes or stop-and-go waves. Moreover, the combination of pedestrian heuristics with body collisions generates crowd turbulence at extreme densities--a phenomenon that has been observed during recent crowd disasters. By proposing an integrated treatment of simultaneous interactions between multiple individuals, our approach overcomes limitations of current physics-inspired pair interaction models. Understanding crowd dynamics through cognitive heuristics is therefore not only crucial for a better preparation of safe mass events. It also clears the way for a more realistic modeling of collective social behaviors, in particular of human crowds and biological swarms. Furthermore, our behavioral heuristics may serve to improve the navigation of autonomous robots.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

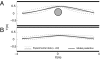
 = 1.3 m/s.
= 1.3 m/s.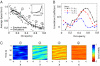
 where the brackets indicate an average over all pedestrians i and over time t (Materials and Methods). (B) Correlation coefficient between the average local speeds V(x,t) and
where the brackets indicate an average over all pedestrians i and over time t (Materials and Methods). (B) Correlation coefficient between the average local speeds V(x,t) and  , measuring the occurrence of stop-and-go waves (see Materials and Methods for the analytical definition of the local speed). Here, the value of X is set to 2 m. The increase at intermediate densities indicates that speed variations at positions x and x − X are correlated for an assumed time delay T of 3 s. Significant P values for the correlation coefficient are found for occupancies between 0.4 and 0.65, indicating the boundaries of the stop-and-go regime (
, measuring the occurrence of stop-and-go waves (see Materials and Methods for the analytical definition of the local speed). Here, the value of X is set to 2 m. The increase at intermediate densities indicates that speed variations at positions x and x − X are correlated for an assumed time delay T of 3 s. Significant P values for the correlation coefficient are found for occupancies between 0.4 and 0.65, indicating the boundaries of the stop-and-go regime ( was chosen according to a normal distribution with mean value 1.3 m/s and SD = 0.2.
was chosen according to a normal distribution with mean value 1.3 m/s and SD = 0.2.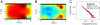
 reveals two critical areas of strong compression in front of the bottleneck (shown in red). (B) Analyzing the “crowd pressure” (defined as local density times the local velocity variance) (Materials and Methods) reveals areas with a high risk of falling (in red), indicating the likelihood of a crowd disaster (4). (C) Distribution of displacements (i.e., location changes between two subsequent stops, defined by speeds with
reveals two critical areas of strong compression in front of the bottleneck (shown in red). (B) Analyzing the “crowd pressure” (defined as local density times the local velocity variance) (Materials and Methods) reveals areas with a high risk of falling (in red), indicating the likelihood of a crowd disaster (4). (C) Distribution of displacements (i.e., location changes between two subsequent stops, defined by speeds with  ). The double logarithmic representation reveals a power law with slope k = −1.95 ± 0.09, in good agreement with empirical findings (see figure 3e in ref. , where the slope is k = −2.01 ± 0.15). The local speed, local pressure, and local compression coefficients are defined in Materials and Methods. The above results are based on simulations of 360 pedestrians during 240 s in a corridor of length l = 10 m and width w = 6 m, with a bottleneck of width 4 m, assuming periodic boundary conditions.
). The double logarithmic representation reveals a power law with slope k = −1.95 ± 0.09, in good agreement with empirical findings (see figure 3e in ref. , where the slope is k = −2.01 ± 0.15). The local speed, local pressure, and local compression coefficients are defined in Materials and Methods. The above results are based on simulations of 360 pedestrians during 240 s in a corridor of length l = 10 m and width w = 6 m, with a bottleneck of width 4 m, assuming periodic boundary conditions.References
-
- Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature. 2000;407:487–490. - PubMed
-
- Schadschneider A, et al. Evacuation dynamics: Empirical results, modeling and applications. In: Meyers R, editor. Encyclopedia of Complexity and Systems Science. Berlin: Springer; 2009. pp. 3142–3176.
-
- Dyer J, et al. Consensus decision making in human crowds. Anim Behav. 2008;75:461–470.
-
- Helbing D, Johansson A, Al-Abideen HZ. Dynamics of crowd disasters: An empirical study. Phys Rev E. 2007;75:046109. - PubMed
-
- Antonini G, Bierlaire M, Weber M. Discrete choice models of pedestrian walking behavior. Transp Res Part B: Methodol. 2006;40:667–687.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

