Electro-osmotic mobility of non-Newtonian fluids

Abstract

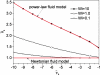
Electrokinetically driven microfluidic devices are usually used to analyze and process biofluids which can be classified as non-Newtonian fluids. Conventional electrokinetic theories resulting from Newtonian hydrodynamics then fail to describe the behaviors of these fluids. In this study, a theoretical analysis of electro-osmotic mobility of non-Newtonian fluids is reported. The general Cauchy momentum equation is simplified by incorporation of the Gouy-Chapman solution to the Poisson-Boltzmann equation and the Carreau fluid constitutive model. Then a nonlinear ordinary differential equation governing the electro-osmotic velocity of Carreau fluids is obtained and solved numerically. The effects of the Weissenberg number (Wi), the surface zeta potential (ψ¯s), the power-law exponent(n), and the transitional parameter (β) on electro-osmotic mobility are examined. It is shown that the results presented in this study for the electro-osmotic mobility of Carreau fluids are quite general so that the electro-osmotic mobility for the Newtonian fluids and the power-law fluids can be obtained as two limiting cases.

Figure 1

Variation of electro-osmotic mobility with the surface zeta potential for three different values of Wi (Wi=0.1,1.0,10.0)when n=0.8 andβ=2. There are also two limiting cases included in the figure: (i) the Newtonian fluid model with the electro-osmotic mobility being unity and (ii) the power-law fluid model with the electro-osmotic mobility computed from Eq. 19.

Figure 2

Variation of electro-osmotic mobility with fluid power-law exponent n for three different values of Wi (Wi=0.1,1.0,10.0)when β=2 and ${\overline{\psi }}_s=-5$. There are also two limiting cases included in the figure: (i) the Newtonian fluid model with the electro-osmotic mobility being unity and (ii) the power-law fluid model with the electro-osmotic mobility computed from Eq. 19.

Figure 3

Variation of electro-osmotic mobility with β for three different values of Wi (Wi=0.1,1.0,10.0) when n=0.8 and ${\overline{\psi }}_s=-5$. There are also two limiting cases included in the figure: (i) the Newtonian fluid model with the electro-osmotic mobility being unity and (ii) the power-law fluid model with the electro-osmotic mobility computed from Eq. 19.