Causality analysis of neural connectivity: critical examination of existing methods and advances of new methods

Abstract

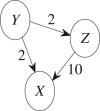
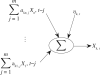
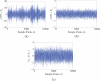
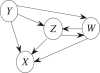
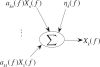
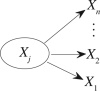
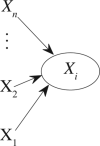
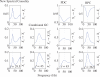
Granger causality (GC) is one of the most popular measures to reveal causality influence of time series and has been widely applied in economics and neuroscience. Especially, its counterpart in frequency domain, spectral GC, as well as other Granger-like causality measures have recently been applied to study causal interactions between brain areas in different frequency ranges during cognitive and perceptual tasks. In this paper, we show that: 1) GC in time domain cannot correctly determine how strongly one time series influences the other when there is directional causality between two time series, and 2) spectral GC and other Granger-like causality measures have inherent shortcomings and/or limitations because of the use of the transfer function (or its inverse matrix) and partial information of the linear regression model. On the other hand, we propose two novel causality measures (in time and frequency domains) for the linear regression model, called new causality and new spectral causality, respectively, which are more reasonable and understandable than GC or Granger-like measures. Especially, from one simple example, we point out that, in time domain, both new causality and GC adopt the concept of proportion, but they are defined on two different equations where one equation (for GC) is only part of the other (for new causality), thus the new causality is a natural extension of GC and has a sound conceptual/theoretical basis, and GC is not the desired causal influence at all. By several examples, we confirm that new causality measures have distinct advantages over GC or Granger-like measures. Finally, we conduct event-related potential causality analysis for a subject with intracranial depth electrodes undergoing evaluation for epilepsy surgery, and show that, in the frequency domain, all measures reveal significant directional event-related causality, but the result from new spectral causality is consistent with event-related time-frequency power spectrum activity. The spectral GC as well as other Granger-like measures are shown to generate misleading results. The proposed new causality measures may have wide potential applications in economics and neuroscience.

Fig. 1

(a) GC values from X₂ to X₁ in (8) as the variance ${\sigma }_{{\eta }_1}^2$ changes from 0.01 to 2 where a_{12, 1} = –0.8. (b) GC values from X₂ to X₁ in (8) as a_{12, 1} changes from –0.1 to –0.95 where ${\sigma }_{{\eta }_1}^2=1$. From (a) one can see that GC value from X₂ to X₁ decreases as the variance ${\sigma }_{{\eta }_1}^2$ increases. From (b) one can see that GC value from X₂ to X₁ increases as the amplitude |a_{12, 1}| increases.

Fig. 2

(a) GC from X₂ to X₁ as a function of the order of the estimated models for (9) when a_{11, 1} = 0.2 and a_{21, 1} changes from 0.1 to 0.9. (b) GC from X₂ to X₁ as a function of the order of the estimated models for (9) when a_{21, 1} = 0.2 and a_{11, 1} changes from 0.1 to 0.9. From (a) and (b), one can see that: 1) GC from X₂ to X₁ keeps steady and converges to 0.67 when the order p > 8, and 2) GC from X₂ to X₁ has nothing to do with parameters a_{11, 1} and a_{21, 1}.

Fig. 3

Connectivities among three time series.

Fig. 4

Contributions to X_k,t .

Fig. 5

Plot of trajectories for –0.99X_2,t, –0.99X̄_2,t, and η_1,t for one realization of (24) and (25) where X_i,0 = X̄_i,0 and ${\eta }_{i,t}={\stackrel{‒}{\eta }}_{i,t}$, i = 1, 2: (a) –0.99 X_2,t 's trajectory for (24). (b) –0.99X̄_2,t 's trajectory for (25)(c) η_1,t 's or ${\stackrel{‒}{\eta }}_{1,t}’\mathrm{s}$ trajectory.

Fig. 6

Connectivities among four time series.

Fig. 7

Contributions to X_k(f).

Fig. 8

X_j's contributions to all signals X_i, i = 1, 2, . . . , n.

Fig. 9

Past contributions to X_i's evolution from all signals X_j, j = 1, 2, . . . , n.

Fig. 10

(a) Spectral GC results: I_X2→X1(f) based on (34) for (39) of two time series in two cases: a_{11, 1} 0.1 and a_{11, 1} = 0.8. (b) New spectral causality results: N_X2→X1(f) for (39).

Fig. 11

New spectral causality results: $N_{X_2\stackrel{\mathrm{D}}{\to }{X}_1}\left(f\right)$ and $N_{X_3\stackrel{\mathrm{D}}{\to }{X}_1}\left(f\right)$ for (40).

Fig. 12

Curve of RPC R_1←3(f) calculated based on (42).

Fig. 13

(a) Results of new causality based on (20) for (43) of three time series in time domain. Self-contributions are neglected. The resulting strength of the connections is schematically represented by the thickness of arrows. (b) New spectral causality from X₃ to X₁ is shown for (43) in frequency domain.

Fig. 14

(a) Power spectra of X₁, X₂, X₃. It can be seen that X₁, X₂, X₃ have almost same powers across all frequencies and have an obvious peak at f = 29.5 Hz. (b) $N\left(f\right)=N_{X_3\stackrel{\mathrm{D}}{\to }{X}_2}\left(f\right)\times N_{X_2\stackrel{\mathrm{D}}{\to }{X}_1}\left(f\right)$ based on (44) and N_T(f) = N_X3→X1 (f) based on the estimated AR model of the pair (X₁, X₃). One can see that N_T(f) (i.e., the total causality from X₃ to X₁) is very close to N(f) (i.e., summation of causalities along all routes from X₃ to X₁) before 40 Hz. But after 40 Hz, N(f) > N_T(f). For a general model, the exact relationship between N(f) and N_T(f) is not known.

Fig. 15

Comparison among new spectral causality, conditional spectral GC, PDC, and RPC together. The first, third, and fourth columns show direct new spectral causality, PDC, and RPC, respectively, from X₁ to X₁, from X₂ to X₁, and from X₃ to X₁. The second column shows conditional GC. It is notable that: 1) new spectral causality from X₁ to X₁, from X₂ to X₁, and from X₃ to X₁ are similar and have peaks at the same frequence of 29.5 Hz, which is consistent with the peak frequency of power spectra [see Fig. 14(a)], and 2) conditional GC, PDC, and RPC (from X₂ to X₁, and from X₃ to X₁) have peaks at different frequencies which are all different from 29.5 Hz.

Fig. 16

(a) ERPs for eight left Macrowire channels (LMacro1–LMacro8) and eight right Macrowire channels (RMacro1–RMacro8) where average reference is applied. (b) Power spectra for LMacro4 (or L4) and RMacro5 (or R5). (c) New spectral causality results between L4 and R5. (d) GC results between L4 and R5. (e) PDC results between L4 and R5. (f) RPC results between L4 and R5.