Switching processes in financial markets
- PMID: 21521789
- PMCID: PMC3093477
- DOI: 10.1073/pnas.1019484108
Switching processes in financial markets
Abstract
For an intriguing variety of switching processes in nature, the underlying complex system abruptly changes from one state to another in a highly discontinuous fashion. Financial market fluctuations are characterized by many abrupt switchings creating upward trends and downward trends, on time scales ranging from macroscopic trends persisting for hundreds of days to microscopic trends persisting for a few minutes. The question arises whether these ubiquitous switching processes have quantifiable features independent of the time horizon studied. We find striking scale-free behavior of the transaction volume after each switching. Our findings can be interpreted as being consistent with time-dependent collective behavior of financial market participants. We test the possible universality of our result by performing a parallel analysis of fluctuations in time intervals between transactions. We suggest that the well known catastrophic bubbles that occur on large time scales--such as the most recent financial crisis--may not be outliers but single dramatic representatives caused by the formation of increasing and decreasing trends on time scales varying over nine orders of magnitude from very large down to very small.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
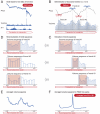

 (t-test, p-value = 9.2 × 10-16) and
(t-test, p-value = 9.2 × 10-16) and  (t-test, p-value < 2 × 10-16). The shaded intervals mark the region in which the empirical data are consistent with a power-law behavior. The left border of the shaded regions is given by the first measuring point closest to the switching point. The right borders stem from statistical tests of the power-law hypothesis (see
(t-test, p-value < 2 × 10-16). The shaded intervals mark the region in which the empirical data are consistent with a power-law behavior. The left border of the shaded regions is given by the first measuring point closest to the switching point. The right borders stem from statistical tests of the power-law hypothesis (see  (t-test, p-value < 2 × 10-16) and
(t-test, p-value < 2 × 10-16) and  (t-test, p-value = 1.7 × 10-9) which are similar to our results on short time scales. (F) Log—log plot of the intertrade times on short time scales (50 ticks ≤ Δt ≤ 100 ticks) exhibits a power-law behavior with exponents
(t-test, p-value = 1.7 × 10-9) which are similar to our results on short time scales. (F) Log—log plot of the intertrade times on short time scales (50 ticks ≤ Δt ≤ 100 ticks) exhibits a power-law behavior with exponents  (t-test, p-value < 2 × 10-16) and
(t-test, p-value < 2 × 10-16) and  (t-test, p-value = 1.8 × 10-15). An equivalent analysis on long time scales is not possible as daily closing prices are recorded with equidistant time steps.
(t-test, p-value = 1.8 × 10-15). An equivalent analysis on long time scales is not possible as daily closing prices are recorded with equidistant time steps.References
-
- Axtell RL. Zipf distribution of U.S. firm sizes. Science. 2001;293:1818–1820. - PubMed
-
- Stanley MHR, et al. Zipf plots and the size distribution of firms. Economics Letters. 1995;49:453–457.
-
- Gabaix X, Gopikrishnan P, Plerou V, Stanley HE. Institutional investors and stock market volatility. Quarterly Journal of Economics. 2006;121:461–504.
-
- Lillo F, et al. Econophysics: master curve for price-impact function. Nature. 2003;421:129–130. - PubMed
-
- Onnela JP, Chakraborti A, Kaski K, Kertesz J, Kanto A. Dynamics of market correlations: Taxonomy and portfolio analysis. Phys Rev E. 2003;68:056110. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources

