Biophysical mechanisms of multistability in resting-state cortical rhythms

Abstract

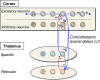
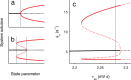
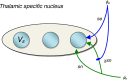
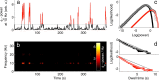
The human alpha (8-12 Hz) rhythm is one of the most prominent, robust, and widely studied attributes of ongoing cortical activity. Contrary to the prevalent notion that it simply "waxes and wanes," spontaneous alpha activity bursts erratically between two distinct modes of activity. We now establish a mechanism for this multistable phenomenon in resting-state cortical recordings by characterizing the complex dynamics of a biophysical model of macroscopic corticothalamic activity. This is achieved by studying the predicted activity of cortical and thalamic neuronal populations in this model as a function of its dynamic stability and the role of nonspecific synaptic noise. We hence find that fluctuating noisy inputs into thalamic neurons elicit spontaneous bursts between low- and high-amplitude alpha oscillations when the system is near a particular type of dynamical instability, namely a subcritical Hopf bifurcation. When the postsynaptic potentials associated with these noisy inputs are modulated by cortical feedback, the SD of power within each of these modes scale in proportion to their mean, showing remarkable concordance with empirical data. Our state-dependent corticothalamic model hence exhibits multistability and scale-invariant fluctuations-key features of resting-state cortical activity and indeed, of human perception, cognition, and behavior-thus providing a unified account of these apparently divergent phenomena.

Figure 1.

Schema of principal neural populations and loops within the corticothalamic model. Connectivity and loops include intracortical (ee, ei, ie, ii), corticothalamic (re, se), thalamocortical (es, is), and intrathalamic (sr, rs). Arrows indicate excitatory feedback (blue) and inhibitory feedback (red).

Figure 2.

Multistability in human EEG data. a, Exemplar time course of the power at 10 Hz (squared wavelet coefficients) shows erratic switching between low-power (black) and high-power (red) modes. b, Corresponding time–frequency plane. c, Probability distributions of power at 10 Hz (gray squares) are closely fitted by the sum (white line) of the two unimodal exponential distributions of low-power (black) and high-power (red) modes. A direct model comparison indicates the superiority of the bimodal fit compared with the unimodal fit [BIC difference (unimodal − bimodal) = 532]. Note that the width of each mode is constant on logarithmic axes, implying that the SD is scale free. The intersection of the exponential distributions provides the threshold used to partition the time series. d, Dwell-time cumulative distributions for the low-power (black) and high-power (red) modes closely follow long-tailed stretched-exponential forms (white lines). The parameter values of the stretched-exponential fits for the dwell-time CDFs of the low- and high-energy mode are a_low = 1.94, a_high = 1.78, b_low = 0.54, and b_high = 0.71. The gray line indicates a simple exponential form. Cumulative distributions were separately rescaled to have a mean value of one.

Figure 3.

Fluctuations in alpha power in the noise-driven corticothalamic model in the presence of a global fixed point attractor. a, Noise-induced fluctuations in the expression of spontaneous alpha power. arb. u., Arbitrary units. b, Probability distribution of power at 10 Hz (gray squares) is closely fitted by a single-exponential distribution.

Figure 4.

a, b, Canonical supercritical (a) and subcritical (b) Hopf bifurcations. Black and red denotes fixed-point and periodic solutions, respectively. Solid and dashed lines indicate stable and unstable solutions, respectively. Vertical gray lines indicate critical values of the tuning parameter. c, Bifurcation diagram for ϕ_e (excitatory synaptic states) obtained from Equations 6–13 using parameter values that yielded the main findings of this study. The instability corresponds to the appearance of an unstable 10 Hz mode and a range of values for ϕ_e, which are physiologically plausible. The gray line indicates the value of ν_se,(the synaptic strength of excitatory cortical projections to the specific thalamic nucleus) used in subsequent simulations.

Figure 5.

Multistability in the corticothalamic model when driven by purely additive noise. a, Noise-induced switching between low- and high-amplitude fluctuations. arb. u., Arbitrary units. b, Probability distributions of power at 10 Hz (gray squares) shows a broad low-power exponential distribution and a high-power mode that is relatively narrow in these logarithmic coordinates. This is because the mean is shifted by two orders of magnitude but the SD is approximately equal to the low-power mode.

Figure 6.

Schema of stochastic inputs ϕ_n (green) into the specific nucleus of the thalamus and their multiplicative modulation by excitatory inputs from the cortex ϕ_e (blue). After synaptodendritic filtering, these inputs cause fluctuations in V_s, the mean membrane potential of thalamic neurons. Note that the arrows denote population projections, not single neurons: the two nonspecific noise inputs are uncorrelated at the population level.

Figure 7.

Multistability in the corticothalamic model when driven by state-dependent thalamic input. The characteristics of the model outcome show a remarkable concordance with empirical EEG data (panels as for Fig. 2). As in the data, the PDF (c) shows a clear bimodal distribution [BIC difference (unimodal − bimodal) = 323]. The parameter values of the stretched-exponential fits for the dwell-time CDFs of the low- and high-energy mode are a_low = 1.53, a_high = 1.29, b_low = 0.66, and b_high = 0.75, closely resembling the fitting parameters of the EEG data. arb. u., Arbitrary units.