Using graph theory to analyze biological networks
- PMID: 21527005
- PMCID: PMC3101653
- DOI: 10.1186/1756-0381-4-10
Using graph theory to analyze biological networks
Abstract
Understanding complex systems often requires a bottom-up analysis towards a systems biology approach. The need to investigate a system, not only as individual components but as a whole, emerges. This can be done by examining the elementary constituents individually and then how these are connected. The myriad components of a system and their interactions are best characterized as networks and they are mainly represented as graphs where thousands of nodes are connected with thousands of vertices. In this article we demonstrate approaches, models and methods from the graph theory universe and we discuss ways in which they can be used to reveal hidden properties and features of a network. This network profiling combined with knowledge extraction will help us to better understand the biological significance of the system.
Figures


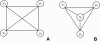


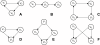
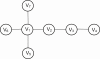
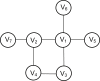


References
-
- Pellegrini Matteo, Haynor David, Johnson JM. Protein interaction networks. Expert Rev Proteomics. 2004;1(2) - PubMed
-
- Vikis HG, Guan KL. Glutathione-S-transferase-fusion based assays for studying protein-protein interactions. Methods Mol Biol. 2004;261:175–186. - PubMed
-
- Puig O, Caspary F, Rigaut G, Rutz B, Bouveret E, Bragado-Nilsson E, Wilm M, Seraphin B. The tandem affinity purification (TAP) method: a general procedure of protein complex purification. Methods. 2001;24(3):218–229. - PubMed
-
- Gavin AC, Bosche M, Krause R, Grandi P, Marzioch M, Bauer A, Schultz J, Rick JM, Michon AM, Cruciat CM. et al. Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature. 2002;415(6868):141–147. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources

