Quantifying the relative contributions of divisive and subtractive feedback to rhythm generation
- PMID: 21533065
- PMCID: PMC3080843
- DOI: 10.1371/journal.pcbi.1001124
Quantifying the relative contributions of divisive and subtractive feedback to rhythm generation
Abstract
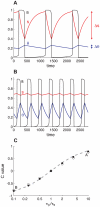
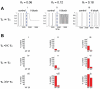
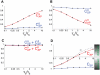
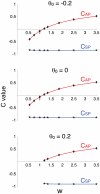
Biological systems are characterized by a high number of interacting components. Determining the role of each component is difficult, addressed here in the context of biological oscillations. Rhythmic behavior can result from the interplay of positive feedback that promotes bistability between high and low activity, and slow negative feedback that switches the system between the high and low activity states. Many biological oscillators include two types of negative feedback processes: divisive (decreases the gain of the positive feedback loop) and subtractive (increases the input threshold) that both contribute to slowly move the system between the high- and low-activity states. Can we determine the relative contribution of each type of negative feedback process to the rhythmic activity? Does one dominate? Do they control the active and silent phase equally? To answer these questions we use a neural network model with excitatory coupling, regulated by synaptic depression (divisive) and cellular adaptation (subtractive feedback). We first attempt to apply standard experimental methodologies: either passive observation to correlate the variations of a variable of interest to system behavior, or deletion of a component to establish whether a component is critical for the system. We find that these two strategies can lead to contradictory conclusions, and at best their interpretive power is limited. We instead develop a computational measure of the contribution of a process, by evaluating the sensitivity of the active (high activity) and silent (low activity) phase durations to the time constant of the process. The measure shows that both processes control the active phase, in proportion to their speed and relative weight. However, only the subtractive process plays a major role in setting the duration of the silent phase. This computational method can be used to analyze the role of negative feedback processes in a wide range of biological rhythms.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


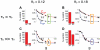

References
-
- van der Pol B, van der Mark J. The heartbeat considered as a relaxation oscillation, and an electrical model of the heart. Phil Mag. 1928;6:763–775.
-
- Rinzel J, Ermentrout B. Analysis of neural excitability and oscillations. In: Koch C, Segev I, editors. Methods in Neuronal Modeling: From Synapses to Networks. Cambridge, MA: MIT Press; 1989.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

