Free energy simulations of a GTPase: GTP and GDP binding to archaeal initiation factor 2

Abstract

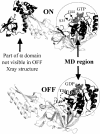
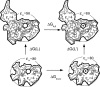
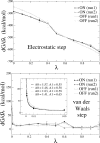
Archaeal initiation factor 2 (aIF2) is a protein involved in the initiation of protein biosynthesis. In its GTP-bound, "ON" conformation, aIF2 binds an initiator tRNA and carries it to the ribosome. In its GDP-bound, "OFF" conformation, it dissociates from tRNA. To understand the specific binding of GTP and GDP and its dependence on the ON or OFF conformational state of aIF2, molecular dynamics free energy simulations (MDFE) are a tool of choice. However, the validity of the computed free energies depends on the simulation model, including the force field and the boundary conditions, and on the extent of conformational sampling in the simulations. aIF2 and other GTPases present specific difficulties; in particular, the nucleotide ligand coordinates a divalent Mg(2+) ion, which can polarize the electronic distribution of its environment. Thus, a force field with an explicit treatment of electronic polarizability could be necessary, rather than a simpler, fixed charge force field. Here, we begin by comparing a fixed charge force field to quantum chemical calculations and experiment for Mg(2+):phosphate binding in solution, with the force field giving large errors. Next, we consider GTP and GDP bound to aIF2 and we compare two fixed charge force fields to the recent, polarizable, AMOEBA force field, extended here in a simple, approximate manner to include GTP. We focus on a quantity that approximates the free energy to change GTP into GDP. Despite the errors seen for Mg(2+):phosphate binding in solution, we observe a substantial cancellation of errors when we compare the free energy change in the protein to that in solution, or when we compare the protein ON and OFF states. Finally, we have used the fixed charge force field to perform MDFE simulations and alchemically transform GTP into GDP in the protein and in solution. With a total of about 200 ns of molecular dynamics, we obtain good convergence and a reasonable statistical uncertainty, comparable to the force field uncertainty, and somewhat lower than the predicted GTP/GDP binding free energy differences. The sign and magnitudes of the differences can thus be interpreted at a semiquantitative level, and are found to be consistent with the experimental binding preferences of ON- and OFF-aIF2.

Figure 1

Thermodynamic cycle for protein:ligand binding. Vertical legs correspond to binding; horizontal legs correspond to the alchemical transformation of the ligand from L into L′, either in the solvated protein (above) or in solution (below). The L/L′ binding free energy difference is ΔΔG = ΔG_prot – ΔG_solv = ΔG_bind(L′) – ΔG_bind(L).

Figure 2

Crystal structures of ON and OFF aIF2. The spherical region included explicitly in the MD model is indicated and colored black; a part of the α domain not seen in the OFF X-ray structure is also indicated. The GTP and GDP ligands are shown (CPK view, colored gray) and labeled. Missing switch 1 residues are indicated by a dashed line; the adjacent residues are shown as spheres and labeled: Ser35 and Gly44 (ON state); Thr34 and Leu49 (OFF state).

Figure 3

Thermodynamic cycle for Mg²⁺:Pi binding, where Pi designates inorganic phosphate. Vertical legs correspond to binding. Horizontal legs correspond to the alchemical transformation of Pi into a ghost particle in solution, in the presence or absence of Mg²⁺. Free energy changes for the different legs are computed by MDFE (2a, 2b, 2a′, 2b′), analytically (1a, 1b, 1a′, 1b′), or known to be zero (leg 0).

Figure 4

Scheme to compute the contribution of distant protein regions to the GTP/GDP binding free energy difference. Poisson–Boltzmann calculations are used to compare the spherically truncated model, limited to the MD region (below), and a larger model, spherically truncated with a 55 Å radius (“full” system, above). The 26 Å radius “MD” sphere is indicated as a dashed line for clarity. Each system is divided into an inner, protein medium, with a dielectric of four, and an outer, solvent medium, with a dielectric of 80. The dielectric boundary is schematized by a thick line. Horizontal legs represent the transformation of GTP by insertion of a positive charge onto its γ phosphate, mimicking the electrostatic step of the GTP → GDP transformation (see main text), and schematized here as the insertion of a “+” sign.

Figure 5

Mg²⁺:phosphate complexes from the quantum chemical model (left), the Charmm27 force field model (upper right), and the Protein Data Bank (lower right). The five quantum structures include Mg²⁺ (on the right, surrounded by 4–6 waters), HPO₄^2– (on the left), and nine water molecules; the structures were energy-minimized at the B3LYP-D/aug-cc-pVDZ level in the presence of a dielectric continuum solvent (see text). Structures IA and IB have a water-mediated Mg²⁺:phosphate interaction; IIA, IIIA, and IIIB have a direct interaction, either mono- or bidentate. The Charmm27 force field structure includes 10 waters that coordinate Mg²⁺ or hydrogen bond to HPO₄^2–. The Mg²⁺:ADP complex (lower right) is from the 3FPS Protein Data Bank entry. It has a bidentate Mg²⁺:phosphate interaction, with distances indicated (in Å).

Figure 6

Above: Free energy derivative ∂G/∂λ for the electrostatic step of the GTP → GDP transformation in the ON and OFF states, as a function of the coupling coordinate, λ. Data for two runs are shown. Uncertainties are shown as vertical bars (often too small to be seen). Below: ∂G/∂λ for the van der Waals step of the transformation. The inset enlarges the region near λ = 0; the smooth curves are fits to the numerical derivatives with the function A₁λ^A₂ (see text).

Figure 7

Sampling during the λ_elec = 0.4 window of run 1, OFF state. Upper left: free energy derivative. Upper right: inverse O:Mg distance, summed over the three terminal GTP oxygens. Bottom left: pseudodihedral angle Φ, defined by the atoms O–P–P′–O′ and highlighted by a dashed line in the bottom right panel. Bottom right: GTP structures representative of the two isomers seen in the dihedral plot.