Robust statistical label fusion through COnsensus Level, Labeler Accuracy, and Truth Estimation (COLLATE)
- PMID: 21536519
- PMCID: PMC3150602
- DOI: 10.1109/TMI.2011.2147795
Robust statistical label fusion through COnsensus Level, Labeler Accuracy, and Truth Estimation (COLLATE)
Abstract
Segmentation and delineation of structures of interest in medical images is paramount to quantifying and characterizing structural, morphological, and functional correlations with clinically relevant conditions. The established gold standard for performing segmentation has been manual voxel-by-voxel labeling by a neuroanatomist expert. This process can be extremely time consuming, resource intensive and fraught with high inter-observer variability. Hence, studies involving characterizations of novel structures or appearances have been limited in scope (numbers of subjects), scale (extent of regions assessed), and statistical power. Statistical methods to fuse data sets from several different sources (e.g., multiple human observers) have been proposed to simultaneously estimate both rater performance and the ground truth labels. However, with empirical datasets, statistical fusion has been observed to result in visually inconsistent findings. So, despite the ease and elegance of a statistical approach, single observers and/or direct voting are often used in practice. Hence, rater performance is not systematically quantified and exploited during label estimation. To date, statistical fusion methods have relied on characterizations of rater performance that do not intrinsically include spatially varying models of rater performance. Herein, we present a novel, robust statistical label fusion algorithm to estimate and account for spatially varying performance. This algorithm, COnsensus Level, Labeler Accuracy and Truth Estimation (COLLATE), is based on the simple idea that some regions of an image are difficult to label (e.g., confusion regions: boundaries or low contrast areas) while other regions are intrinsically obvious (e.g., consensus regions: centers of large regions or high contrast edges). Unlike its predecessors, COLLATE estimates the consensus level of each voxel and estimates differing models of observer behavior in each region. We show that COLLATE provides significant improvement in label accuracy and rater assessment over previous fusion methods in both simulated and empirical datasets.
© 2011 IEEE
Figures



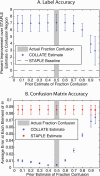
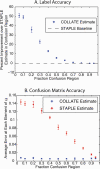



References
-
- Warfield S, et al. Automatic identification of gray matter structures from MRI to improve the segmentation of white matter lesions. J Image Guid Surg. 1995;1:326–38. - PubMed
-
- Kikinis R, et al. Routine quantitative analysis of brain and cerebrospinal fluid spaces with MR imaging. J Magn Reson Imaging. 1992 Nov-Dec;2:619–29. - PubMed
-
- Ho TK, et al. Decision Combination in Multiple Classifier Systems. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1994 Jan;16:66–75.
-
- Kittler J, et al. On combining classifiers. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1998 Mar;20:226–239.
-
- Windridge D, Kittler J. A morphologically optimal strategy for classifier combination: Multiple expert fusion as a tomographic process. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2003 Mar;25:343–353.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

