A dimensionless number for understanding the evolutionary dynamics of antigenically variable RNA viruses
- PMID: 21543353
- PMCID: PMC3203497
- DOI: 10.1098/rspb.2011.0435
A dimensionless number for understanding the evolutionary dynamics of antigenically variable RNA viruses
Abstract
Antigenically variable RNA viruses are significant contributors to the burden of infectious disease worldwide. One reason for their ubiquity is their ability to escape herd immunity through rapid antigenic evolution and thereby to reinfect previously infected hosts. However, the ways in which these viruses evolve antigenically are highly diverse. Some have only limited diversity in the long-run, with every emergence of a new antigenic variant coupled with a replacement of the older variant. Other viruses rapidly accumulate antigenic diversity over time. Others still exhibit dynamics that can be considered evolutionary intermediates between these two extremes. Here, we present a theoretical framework that aims to understand these differences in evolutionary patterns by considering a virus's epidemiological dynamics in a given host population. Our framework, based on a dimensionless number, probabilistically anticipates patterns of viral antigenic diversification and thereby quantifies a virus's evolutionary potential. It is therefore similar in spirit to the basic reproduction number, the well-known dimensionless number which quantifies a pathogen's reproductive potential. We further outline how our theoretical framework can be applied to empirical viral systems, using influenza A/H3N2 as a case study. We end with predictions of our framework and work that remains to be done to further integrate viral evolutionary dynamics with disease ecology.
Figures

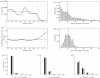
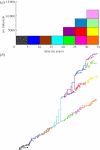

References
-
- Holmes E. C., Grenfell B. T. 2009. Discovering the phylodynamics of RNA viruses. PLoS Comput. Biol. 5, e1000505. 10.1371/journal.pcbi.1000505 (doi:10.1371/journal.pcbi.1000505) - DOI - PMC - PubMed
-
- Rott N. 1990. Note on the history of the Reynolds number. Ann. Rev. Fluid Mech. 22, 1–11 10.1146/annurev.fl.22.010190.000245 (doi:10.1146/annurev.fl.22.010190.000245) - DOI
-
- Anderson R. M., May R. M. 1991. Infectious diseases of humans: dynamics and control. Oxford, UK: Oxford University Press
-
- Grenfell B. T., Pybus O. G., Gog J. R., Wood J. L. N., Daly J. M., Mumford J. A., Holmes E. D. C. 2004. Unifying the epidemiological and evolutionary dynamics of pathogens. Science 303, 327–332 10.1126/science.1090727 (doi:10.1126/science.1090727) - DOI - PubMed
-
- Andreasen V., Sasaki A. 2006. Shaping the phylogenetic tree of influenza by cross-immunity. Theoret. Popul. Biol. 70, 164–173 10.1016/j.tpb.2006.04.004 (doi:10.1016/j.tpb.2006.04.004) - DOI - PubMed
